Cho phương trình x 2 - 2(m + 3)x + m 2 + 3 = 0
c) Tính P = x 1 2 + x 2 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a.\Leftrightarrow mx^2+2mx-x+m+2=0\)
\(\Leftrightarrow mx\left(x+2\right)+\left(m+2\right)-x=0\)
\(\Leftrightarrow\left(m+2\right)\left(mx+1\right)-x=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=\left(0+x\right):\left(mx+1\right)-2\\m=[\left(0+x\right):\left(m+2\right)-1]:x\end{matrix}\right.\)

phương trình này ạ (2m-1)x^2+(m-3)x-6m-2=0 , phương trình trên mình sửa nó lỗi nên viết xuống đây ạ
\(\left(2m-1\right)x^2+\left(m-3\right)x-6m-2=0\)
\(\Leftrightarrow2mx^2-x^2+mx-3x-6m-2=0\)
\(\Leftrightarrow m\left(2x^2+x-6\right)-\left(x^2+3x+2\right)=0\)
\(\Leftrightarrow m\left(2x-3\right)\left(x+2\right)-\left(x+1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left[m\left(2x-3\right)-\left(x+1\right)\right]=0\)
\(\Leftrightarrow\left(x+2\right)\left(\left(2m-1\right)x-3m-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\\left(2m-1\right)x-3m-1=0\end{matrix}\right.\)
\(\Rightarrow\) Pt luôn có nghiệm \(x=-2\) với mọi m
- Nếu \(2m-1=0\Leftrightarrow m=\dfrac{1}{2}\) pt chỉ có nghiệm duy nhất \(x=-2\)
- Nếu \(m\ne\dfrac{1}{2}\) thì nghiệm còn lại thỏa mãn:
\(\left(2m-1\right)x=3m+1\)
\(\Rightarrow x=\dfrac{3m+1}{2m-1}\)

(x2−2x+1+2)(2x−x2−1+7)=18(x2-2x+1+2)(2x-x2-1+7)=18
⇒[(x−1)2+2][7−(x−1)2]=18(1)⇒[(x-1)2+2][7-(x-1)2]=18(1)
Đặt (x−1)2=a(x-1)2=a
(1)⇔(a+2)(7−a)=18(1)⇔(a+2)(7-a)=18
⇒−a2+5a+14=18⇒-a2+5a+14=18
⇒a2−5a+4=0⇒a2-5a+4=0
Ta có a+b+c=1−5+4=0a+b+c=1-5+4=0
⇒a1=1⇒a1=1
a2=41=4a2=41=4
Thay (x−1)2=a(x-1)2=a vào ta được
[(x−1)2=1(x−1)2=4[(x−1)2=1(x−1)2=4
⇒⎡⎢ ⎢ ⎢⎣x−1=1x−1=−1x−1=2x−1=−2⇒[x−1=1x−1=−1x−1=2x−1=−2
⇒⎡⎢ ⎢ ⎢⎣x=2x=0x=3x=−1⇒[x=2x=0x=3x=−1
Vậy nghiệm của phương trình là x={−1;0;2;3}

a) 1 , 5 x 2 – 1 , 6 x + 0 , 1 = 0
Có a = 1,5; b = -1,6; c = 0,1
⇒ a + b + c = 1,5 – 1,6 + 0,1 = 0
⇒ Phương trình có hai nghiệm x 1 = 1 ; x 2 = c / a = 1 / 15 .

d) ( m – 1 ) x 2 – ( 2 m + 3 ) x + m + 4 = 0
Có a = m – 1 ; b = - (2m + 3) ; c = m + 4
⇒ a + b + c = (m – 1) – (2m + 3) + m + 4 = m -1 – 2m – 3 + m + 4 = 0
⇒ Phương trình có hai nghiệm 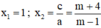

a: \(\Delta=\left(2m-6\right)^2-4\cdot1\cdot\left(m-3\right)\)
\(=4m^2-24m+36-4m+12\)
\(=4m^2-28m+48\)
\(=4\left(m-3\right)\left(m-4\right)\)
Để phương trình có nghiệm kép thì (m-3)(m-4)=0
=>m=3 hoặc m=4
b: Trường hợp 1: m=7/2
Phương trình sẽ là \(2\cdot\left(2\cdot\dfrac{7}{2}+5\right)x-14\cdot\dfrac{7}{2}+1=0\)
\(\Leftrightarrow24x-48=0\)
hay x=2
=>Nhận
Trường hợp 2: m<>7/2
\(\Delta=\left(4m+10\right)^2-4\cdot\left(2m-7\right)\left(-14m+1\right)\)
\(=16m^2+80m+100-4\left(-28m^2+2m+98m-7\right)\)
\(=16m^2+80m+100+112m^2-400m+28\)
\(=128m^2-320m+128\)
\(=64\left(2m^2-5m+2\right)\)
Để phương trình có hai nghiệm phân biệt thì (2m-1)(m-1)=0
=>m=1 hoặc m=1/2

a. m2 ≥ 0 ∀ m
=> m2 +1> 0 ∀ m
b. m2 +2m +3 = m2 + 2m +1 +2 = (m + 1)2 + 2 > 0 ∀ m
c. m2 ≥ 0 ∀ m
=> m2 +2> 0 ∀ m
d. m2 - 2m +2 = m2 -2m + 1 +1 = (m - 1)2 + 1 > 0 ∀ m
a) Để phương trình \(\left(m^2+1\right)x-3=0\) là phương trình bậc nhất một ẩn thì \(m^2+1\ne0\)
\(\Leftrightarrow m^2\ne-1\)
mà \(m^2\ge0\forall m\)
nên \(m^2\ne-1\forall m\)
\(\Leftrightarrow m^2+1\ne0\forall m\)
Vậy: Phương trình \(\left(m^2+1\right)x-3=0\) là phương trình bậc nhất một ẩn với mọi giá trị của tham số m
b) Để phương trình \(\left(m^2+2m+3\right)x+m-1=0\) là phương trình bậc nhất một ẩn thì \(m^2+2m+3\ne0\)
\(\Leftrightarrow\left(m+1\right)^2+2\ne0\)
mà \(\left(m+1\right)^2+2\ge2>0\forall m\)
nên \(\left(m+1\right)^2+2\ne0\forall m\)
hay \(m^2+2m+3\ne0\forall m\)
Vậy: Phương trình \(\left(m^2+2m+3\right)x+m-1=0\) luôn là phương trình bậc nhất một ẩn với mọi tham số m
c) Để phương trình \(\left(m^2+2\right)x-4=0\) là phương trình bậc nhất một ẩn thì \(m^2+2\ne0\)
\(\Leftrightarrow m^2\ne-2\)
mà \(m^2\ge0\forall m\)
nên \(m^2\ne-2\forall m\)
\(\Leftrightarrow m^2+2\ne0\forall m\)
Vậy: Phương trình \(\left(m^2+2\right)x+4=0\) là phương trình bậc nhất một ẩn với mọi giá trị của tham số m
d) Để phương trình \(\left(m^2-2m+2\right)x+m=0\) là phương trình bậc nhất một ẩn thì \(m^2-2m+2\ne0\)
\(\Leftrightarrow\left(m-1\right)^2+1\ne0\)
mà \(\left(m-1\right)^2+1\ge1>0\forall m\)
nên \(\left(m-1\right)^2+1\ne0\forall m\)
hay \(m^2-2m+2\ne0\forall m\)
Vậy: Phương trình \(\left(m^2-2m+2\right)x+m=0\) luôn là phương trình bậc nhất một ẩn với mọi tham số m

Bài 3:
b: \(\Leftrightarrow x^2\left(x+1\right)^2=0\)
hay \(x\in\left\{0;-1\right\}\)
c: \(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)=0\)
=>x-1=0
hay x=1
d: \(\Leftrightarrow6x^2-3x-4x+2=0\)
\(\Leftrightarrow\left(2x-1\right)\left(3x-2\right)=0\)
hay \(x\in\left\{\dfrac{1}{2};\dfrac{2}{3}\right\}\)

a:
ĐKXĐ: \(x\notin\left\{\dfrac{3}{2};1\right\}\)
\(y=\dfrac{\left(x-2\right)^2}{\left(2x-3\right)\left(x-1\right)}=\dfrac{x^2-4x+4}{2x^2-2x-3x+3}\)
=>\(y=\dfrac{x^2-4x+4}{2x^2-5x+3}\)
=>\(y'=\dfrac{\left(x^2-4x+4\right)'\left(2x^2-5x+3\right)-\left(x^2-4x+4\right)\left(2x^2-5x+3\right)'}{\left(2x^2-5x+3\right)^2}\)
=>\(y'=\dfrac{\left(2x-4\right)\left(2x^2-5x+3\right)-\left(2x-5\right)\left(x^2-4x+4\right)}{\left(2x^2-5x+3\right)^2}\)
=>\(y'=\dfrac{4x^3-10x^2+6x-8x^2+20x-12-2x^3+8x^2-8x+5x^2-20x+20}{\left(2x^2-5x+3\right)^2}\)
=>\(y'=\dfrac{2x^3-5x^2-2x+8}{\left(2x^2-5x+3\right)^2}\)
b:
ĐKXĐ: x<>-3
\(y=\left(x+3\right)+\dfrac{4}{x+3}\)
=>\(y'=\left(x+3+\dfrac{4}{x+3}\right)'=1+\left(\dfrac{4}{x+3}\right)'\)
\(=1+\dfrac{4'\left(x+3\right)-4\left(x+3\right)'}{\left(x+3\right)^2}\)
=>\(y'=1+\dfrac{-4}{\left(x+3\right)^2}=\dfrac{\left(x+3\right)^2-4}{\left(x+3\right)^2}\)
y'=0
=>\(\left(x+3\right)^2-4=0\)
=>\(\left(x+3+2\right)\left(x+3-2\right)=0\)
=>(x+5)(x+1)=0
=>x=-5 hoặc x=-1
c:
ĐKXĐ: x<>-2
\(y=\dfrac{\left(5x-1\right)\left(x+1\right)}{x+2}\)
=>\(y=\dfrac{5x^2+5x-x-1}{x+2}=\dfrac{5x^2+4x-1}{x+2}\)
=>\(y'=\dfrac{\left(5x^2+4x-1\right)'\left(x+2\right)-\left(5x^2+4x-1\right)\left(x+2\right)'}{\left(x+2\right)^2}\)
=>\(y'=\dfrac{\left(5x+4\right)\left(x+2\right)-\left(5x^2+4x-1\right)}{\left(x+2\right)^2}\)
=>\(y'=\dfrac{5x^2+10x+4x+8-5x^2-4x+1}{\left(x+2\right)^2}\)
=>\(y'=\dfrac{10x+9}{\left(x+2\right)^2}\)
\(y'\left(-1\right)=\dfrac{10\cdot\left(-1\right)+9}{\left(-1+2\right)^2}=\dfrac{-1}{1}=-1\)
d:
ĐKXĐ: x<>2
\(y=x-2+\dfrac{9}{x-2}\)
=>\(y'=\left(x-2+\dfrac{9}{x-2}\right)'=1+\left(\dfrac{9}{x-2}\right)'\)
\(=1+\dfrac{9'\left(x-2\right)-9\left(x-2\right)'}{\left(x-2\right)^2}\)
=>\(y'=1+\dfrac{-9}{\left(x-2\right)^2}=\dfrac{\left(x-2\right)^2-9}{\left(x-2\right)^2}\)
y'=0
=>\(\dfrac{\left(x-2\right)^2-9}{\left(x-2\right)^2}=0\)
=>\(\left(x-2\right)^2-9=0\)
=>(x-2-3)(x-2+3)=0
=>(x-5)(x+1)=0
=>x=5 hoặc x=-1
c) Theo định lí Vi-et ta có:
P = x 1 2 + x 2 2 = (x1 + x2 )2 - 2 x 1 x 2 = 4 m + 3 2 - 2( m 2 + 3)
= 4( m 2 + 6m + 9) - 2( m 2 + 3) = 2 m 2 + 24m + 30