Cho hàm số f x = 0 k h i x = π 2 + k π , k ∈ ℤ 1 2 + tan 2 x
Tìm điều kiện của a để hàm số g x = f x + f a x tuần hoàn
A. a ∈ Z
B. a ∈ Q
C. a ∈ N
D. a ∈ 0 ; + ∞
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có f ( π ) - f ( 0 ) = ∫ 0 π f ' ( x ) dx
f ( π ) = f ( 0 ) + ∫ 0 π f ' ( x ) dx = π + 1
Chọn đáp án C.

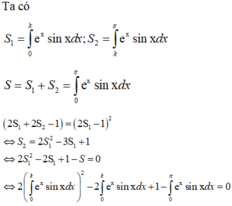
Tính toán trực tiếp qua các đáp án ta thấy PT trên đúng với k = π 2
Đáp án B
Xét hàm số
- Nếu a = p q với p ∈ Z , q ∈ N * thì T = q π là chu kì của g(x)
Vì g x + q π = f x + q π + f a x + p π còn π là chu kì của hàm số f(x)
- Ta sẽ chứng minh nếu a là số vô tỉ thì g(x) không tuần hoàn
Để ý rằng g 0 = f 0 + f 0 = 1 . Nếu g x 0 = 1 đối với x 0 ≠ 0 nào đó thì tan 2 x 0 = 0 và tan 2 a x 0 = 0 . Điều này có nghĩa là x 0 = k π và a x 0 = l π với k , l ∈ Z
Nhưng x 0 ≠ 0 nghĩa là a = 1 k . Điều này mâu thuẫn vì a là số vô tỉ. Do đó hàm số g(x) nhận giá trị 1 tại điểm duy nhất x = 0. Như vậy f(x) sẽ không tuần hoàn
Đáp án B