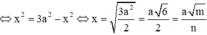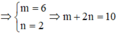Cho n ∈ ℕ * và 1 + x n = a n + a 1 x + . . . + a n x n . Biết rằng tồn tại số nguyên k 1 ≤ k ≤ n - 1 sao cho a k - 1 2 = a k 9 = a k + 1 24 .Tính n?
A. 10
B. 11
C. 20
D. 22
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

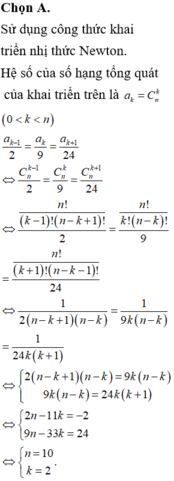

Chọn A.
Phương pháp: Sử dụng công thức khai triển nhị thức Newton.
Cách giải: Hệ số của số hạng tổng quát của khai triển trên là a k = C n k
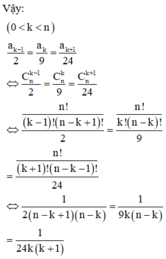
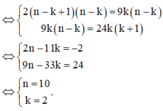

a) \(\left|x+11\right|+\left|13-x\right|=0\)
\(\Rightarrow\hept{\begin{cases}x+11=0\\13-x=0\end{cases}\Rightarrow\hept{\begin{cases}x=-11\\x=13\end{cases}}}\)
Câu b xét dấu trong // nha bạn

Chọn D
Đạo hàm hai vế f(x)
![]()
![]()
![]()
Số hạng tổng quát thứ k + 1 trong khai triển thành đa thức của ![]()
![]()

Đáp án A
Phương pháp:
+) Chứng minh hình chiếu vuông của S trên (ABCD) trùng với tâm đường tròn ngoại tiếp tam giác ABD.
+) Chứng minh tam giác SAC vuông tại S, tính AC.
+) Tính BD.
+) Sử dụng công thức tính thể tích V S . A B C D = 1 3 S H . S A B C D = 1 3 S H . 1 2 A C . B D
Cách giải:
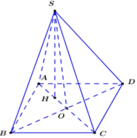
Vì SA = SB = SD = a nên hình chiếu vuông của S trên (ABCD) trùng với tâm đường tròn ngoại tiếp tam giác ABD.
Gọi H là tâm đường tròn ngoại tiếp tam giác ABD
⇒ S H ⊥ ( A B C D ) .
Do tam giác ABD cân tại A ⇒ H ∈ A C
Dễ dàng chứng minh được:
△ S B D = △ A B D ( c . c . c ) ⇒ S O = A O = A C 2 ⇒ △ S A C vuông tại S (Tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh ấy)
![]()
Áp dụng hệ thức lượng trong tam giác vuông SAC có S H = S A . S C A C = a x a 2 + x 2
Ta có
![]()
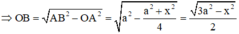
![]()
![]()
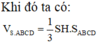
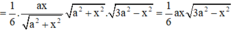
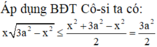
![]()
Dấu “=” xảy ra