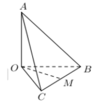
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA=OB=OC. Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng M và AB bằng
A. 60 o
B. 30 o
C. 60 o
D. 45 o
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
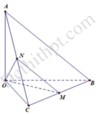
Do OA,OB,OC đội một vuông góc với nhau và O A = O B = O C nên tam giác ABC là tam giác đều. Qua M kẻ đường thẳng song song với AB cắt AC tại N
Ta có M N / / A B ⇒ O M , A B = O M , M N ^ ^
Giả sử O A = O B = O C = a ⇒ A B = B C = C A = a 2
Ta có O M = B C 2 = a 2 2 , O N = A C 2 = a 2 2 , M N = A B 2 = a 2 2
⇒ Δ A B C là tam giác đều ⇒ O M N ^ = 60 0
⇒ O M , M N ^ = 60 0 .

Gọi N là trung điểm của AC ⇒ M N / / A B , Vậy
( OM,AB ) = ( OM,MN ) = OMN
Cho OA = OB = OC = 1. Ta có.
M N = A B 2 = 2 2 O M = B C 2 = 2 2 O N = A C 2 = 2 2
Vậy ∆ O M N là tam giác đều và O M N = 60 o
Đáp án cần chọn là C

Đáp án C
Cách 1.
Gọi N là trung điểm của AC ⇒ M N / / A B
![]()
Cho OA =OB =OC =1. Ta có.

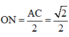
Vậy ∆ O M N là tam giác đều và O M N = 60 o
Cách 2. Dùng pp tọa độ hóa và công thức

Đáp án C.