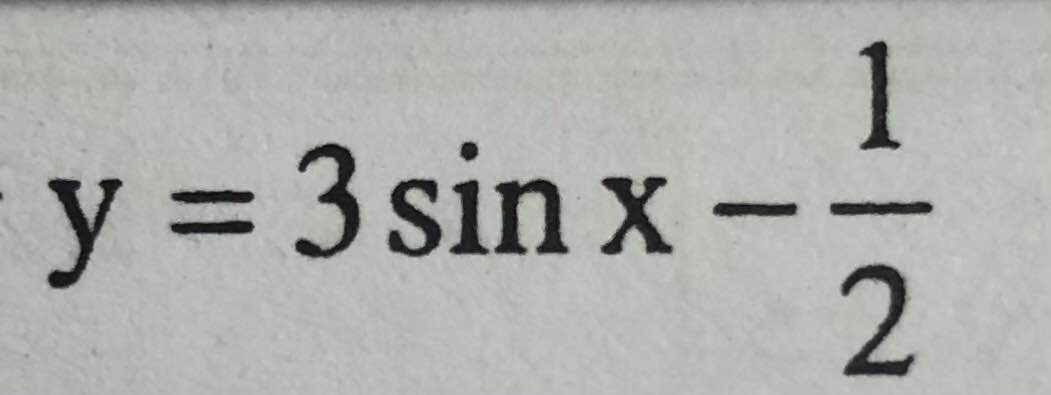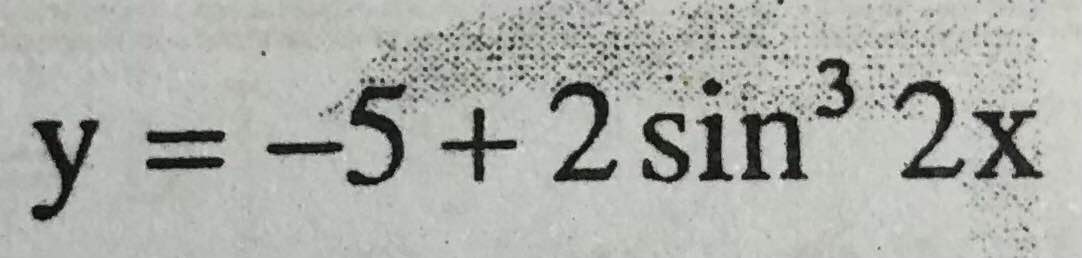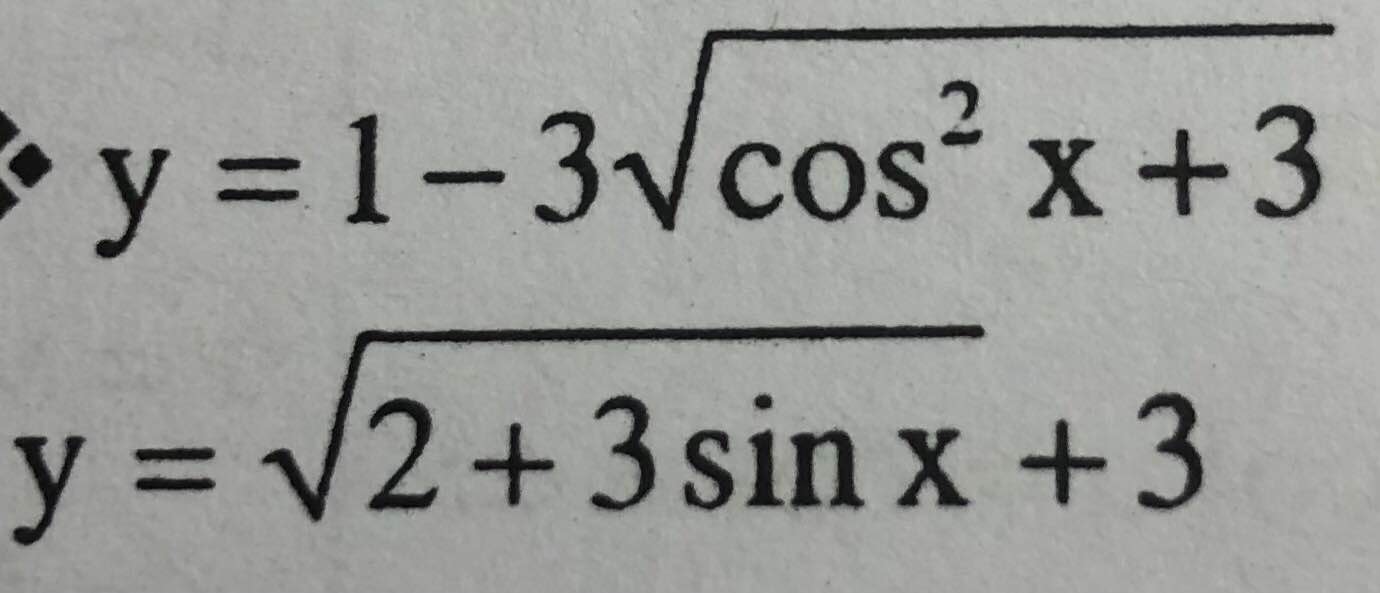Giái trị của x biết : (2x+24).53=4.55
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
\(y=3sinx-\dfrac{1}{2}\)
Do \(-1\le sinx\le1\Rightarrow-3\le3sinx\le3\)
\(\Rightarrow-\dfrac{7}{2}\le3sinx-\dfrac{1}{2}\le\dfrac{5}{2}\)
\(\Rightarrow y_{max}=\dfrac{5}{2}\) ; \(y_{min}=-\dfrac{7}{2}\)
b.
\(y=-5+2sin^32x\)
Do \(-1\le sin2x\le1\Rightarrow-1\le sin^32x\le1\)
\(\Rightarrow-2\le2sin^32x\le2\)
\(\Rightarrow-7\le y\le-3\)
\(y_{max}=-3\) ; \(y_{min}=-7\)
c.
\(0\le cos^2x\le1\Rightarrow3\le cos^2x+3\le4\)
\(\Rightarrow-2\le-\sqrt{cos^2x+3}\le-\sqrt{3}\)
\(\Rightarrow-5\le y\le1-3\sqrt{3}\)
\(y_{min}=-5\) ; \(y_{max}=1-3\sqrt{3}\)
d.
Do tính chất căn thức ta có \(\sqrt{2+3sinx}\ge0\)
\(sinx\le1\Rightarrow3sinx\le3\Rightarrow2+3sin\le5\)
\(\Rightarrow3\le y\le3+\sqrt{5}\)
\(y_{min}=3\) ; \(y_{max}=3+\sqrt{5}\)

a) Ta thấy :x\(^3\)+8=x^3+2^3=(x+2).(x^2-2x+4)
ĐKXD là : (x+2).(x^2-2x+4) # 0 (# là khác )
Ta có :x^2-2x+4=(x^2-2x+1)+3=(x-1)^2+3>3 với mọi x\(\in\) R
Vậy ĐKXD là :x+2\(\ne\)0 => x\(\ne\)-2
b)\(\frac{2x^2-4x+8}{x^3+8}\)=\(\frac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2+4\right)}\)=\(\frac{2}{x+2}\)
c) x=2 (t/m điều kiện ) thay x=2 vào biếu thức trên ta đc :
\(\frac{2}{x+2}\)=\(\frac{2}{4}\)=\(\frac{1}{2}\)
Vậy khi x=2 thì gtrij của biếu thức =\(\frac{1}{2}\)
d) Để phân thức =2 thì \(\frac{2}{x+2}\)=2 <=> \(\frac{2}{x+2}\)=\(\frac{2\left(x+2\right)}{x+2}\)
<=> 2=2x+4
<=> -2=2x <=> x=-1 (t/m điều kiện )
Vậy để phân thức =2 thì x=-1
a. ĐKXĐ: \(x^3+8\ne0\Leftrightarrow\left(x+2\right)\left(x^2-2x+4\right)\ne0\Leftrightarrow x+2\ne0\Leftrightarrow x\ne-2\)
b. \(\frac{2x^2-4x+8}{x^3+8}=\frac{2.\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}=\frac{2}{x+2}\)
c. Tại x = 2, phân thức có giá trị:
\(\frac{2}{2+2}=\frac{2}{4}=\frac{1}{2}\)
d. Để p.thức có giá trị bằng 2 thì:
\(\frac{2}{x+2}=2\Leftrightarrow x+2=1\Leftrightarrow x=-1\)
Vậy để p thức có giá trị bằng 2 thì x = -1.

4.\(5^5\)-32:\(2^4\)-452-(-67+75-452)
=4.25-32:16-452-67-75+452
\(4\cdot5^4-32:2^4-452-\left(-67+75-452\right)\)
\(=4\cdot625-32:16-452+67-75+452\)
\(=2500-2+67-75\)
=2500-2-8
=2500-10
=2490

Biến đổi \(D=\frac{4-x+10}{4-x}=1+\frac{10}{4-x}\).
D lớn nhất khi và chỉ khi \(\frac{10}{4-x}\) lớn nhất.
Xét \(x>4\) thì \(\frac{10}{4-x}< 0.\left(1\right)\)
Xét \(x< 4\) thì \(\frac{10}{4-x}>0\). Phân số \(\frac{10}{4-x}\) có tử và mẫu đều dương, tử không đổi nên có giá trị lớn nhất khi mẫu nhỏ nhất. Mẫu \(4-x\) là số nguyên dương, nhỏ nhất khi \(4-x=1\) tức là \(x=3\). Khi đó
\(\frac{10}{4-x}=10\left(2\right)\)
So sánh \(\left(1\right)\) và \(\left(2\right)\), ta thấy \(\frac{10}{4-x}\) lớn nhất bằng 10. Vậy GTLN của D bằng 11 khi và chỉ khi \(x=3\)
ĐK: \(x\ne4\)
Để D lớn nhất thì 2D lớn nhất
Ta có: \(2D=\frac{2.\left(14-x\right)}{4-x}=\frac{28-2x}{4-x}=\frac{20}{4-x}+\frac{2.\left(4-x\right)}{4-x}=\frac{20}{4-x}+2\)
2D lớn nhất nên \(\frac{20}{4-x}\) lớn nhất hay 4 - x nhỏ nhất
+ Nếu x > 4 thì 4 - x < 0 => \(\frac{20}{4-x}\) < 0 (1)
+ Nếu x < 4 do 4 - x nhỏ nhất; x nguyên nên x = 3 => \(\frac{20}{4-x}=\frac{20}{4-3}=20\) (2)
So sánh (1) với (2) ta thấy (2) lớn hơn
Khi x = 3 thì \(D=\frac{14-3}{4-3}=\frac{11}{1}=11\)
Vậy GTNN của D là 11 khi x = 3