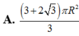
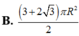
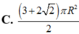
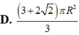
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án B
+ Gọi h, r lần lượt là chiều cao và bán kính đường tròn đáy của hình trụ.
Khi đó, bán kính mặt cầu ngoại tiếp hình trụ là
+ Theo bài ra, ta có h = r nên suy ra
+ Diện tích toàn phần hình trụ là:
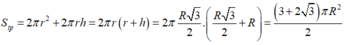
Chọn B.
Phương pháp: Coi đáy của hình trụ là mặt phẳng cắt mặt cầu. Áp dụng công thức
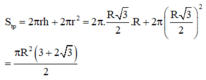
Đáp án B
Gọi h, r lần lượt là chiều cao và bán kính đường tròn đáy của hình trụ.
Khi đó, bán kính mặt cầu ngoại tiếp hình trụ là R 2 = r 2 + h 2 4
Theo bài ra, ta có h = R nên suy ra R 2 = r 2 + h 2 4 ⇔ r 2 = 3 R 2 4 ⇔ r = R 3 2
Diện tích toàn phần hình trụ là:
S t p = 2 πr 2 + 2 πrh = 2 πr r + h = 2 π . R 3 2 . R 3 2 + R = 3 + 2 3 πR 2 2 .
Theo đề bài, tổng diện tích nửa mặt cầu và diện tích hình tròn đáy gấp 3 lần diện tích toàn phần của hình trụ nên:
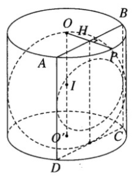
Đường tròn giao tuyến của mặt cầu đường kính OO’ và mặt phẳng (ABCD) có bán kính bằng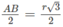 
. Đường tròn này có tâm là tâm của hình chữ nhật ABCD và tiếp xúc với hai cạnh AD, BC của hình chữ nhật đó.
a) Giá trị gần đúng của h là : 10,5 cm
b) Giá trị của r là : 24 cm
Chọn B