Hàm số y = x 2 - x + 1 x - 1 nghịch biến trên các khoản
A. (0; 2) và (2; +∞)
B. (-∞; 0) và (2; +∞)
C. [0; 1) và (1; 2]
D. (0; 1) và (1; 2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=x^2-2x+1=\left(x-1\right)^2\ge0\) ;\(\forall x\in R\)
\(\Rightarrow\) Hàm đồng biến trên R
cho ham số bật nhất y=(2m-3)x+5. Tìm các giá trị cua m hàm số
a/ Đồng biến
b/ Nghịch biến

Chú ý ; Hàm số có dạng y = ax + b (a khác 0) đồng biến khi a > 0 , nghịch biến khi a < 0
Vậy :
a/ Hàm số đồng biến khi 2m-3 > 0 => m > 3/2
b/ Hàm số nghịch biến khi 2m-3 < 0 => m < 3/2

Lời giải:
a. Để hàm số nghịch biến trên R thì:
$a+2<0$
$\Leftrightarrow a< -2$
b.
Để $(d)$ đi qua $M(-1;-4)$ thì:
$y_M=(a+2)x_M-a+1$
$\Leftrightarrow -4=(a+2)(-1)-a+1$
$\Leftrightarrow a=\frac{3}{2}$

ĐKXĐ: \(x\in\left[0;2018\right]\)
\(y'=\dfrac{1009-x}{\sqrt{2018x-x^2}}=0\Rightarrow x=1009\)
Hàm đồng biến trên \(\left(0;1009\right)\)

Đáp án C
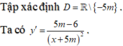
Để hàm số nghịch biến trên khoảng ( 10 ; + ∞ ) thì
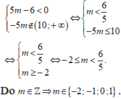
Chọn C