Cho hình dưới đây. Chọn đáp án sai
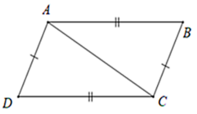
A. A D / / B C
B. A B / / C D
C. Δ A B C = Δ C D A
D. Δ A B C = Δ A D C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Xét ΔAOD và ΔBOC có
OA/OB=OD/OC
góc AOD chung
Do đó: ΔAOD\(\sim\)ΔBOC

a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6

a: Xét ΔAMB và ΔCMD có
MA=MC
góc AMB=góc CMD
MB=MD
Do đó: ΔAMB=ΔCMD
b: ΔAMB=ΔCMD
nên AB=CD và góc MAB=góc MCD
=>AB//CD
c: Xét tứ giác AKBC có
N là trung điểm chung của AB và KC
nên AKBC là hình bình hành
=>AK//BC
Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
nên ABCD là hình bình hành
=>AD//BC
mà AK//BC
nên D,A,K thẳng hàng


a) Chứng minh: AD = BC.
Xét ∆OAD và ∆OBC có:
OA = OB (gt);
ˆAODAOD^ chung;
OD = OC (gt)
Do đó ∆OAD = ∆OBC (c.g.c)
Suy ra AD = BC (hai cạnh tương ứng)
b) Chứng minh: ∆EAC = ∆EBD.
Vì ∆OAD = ∆OBC (câu a)
Nên ˆA2=ˆB2A^2=B^2 (hai góc tương ứng)
Mà ˆA1+ˆA2=180oA^1+A^2=180o, ˆB1+ˆB2=180oB^1+B^2=180o (kề bù)
Do đó ˆA1=ˆB1A^1=B^1.
Mặt khác, OA = OB, OC = OD
Suy ra OC – OA = OD – OB
Do đó AC = BD
Xét ∆EAC và ∆EBD có:
ˆA1=ˆB1A^1=B^1 (cmt);
AC = BD (cmt);
ˆOCB=ˆODAOCB^=ODA^ (vì ∆OAD = ∆OBC)
Do đó ∆EAC = ∆EBD (g.c.g).
c) Chứng minh: OE là tia phân giác của góc xOy.
Vì ∆EAC = ∆EBD (câu b)
Nên AE = BE (hai cạnh tương ứng).
Xét ∆OAE và ∆OBE có:
OA = OB (gt);
Cạnh OE chung;
AE = BE (cmt)
Do đó ∆OAE và ∆OBE (c.c.c)
Suy ra ˆAOE=ˆBOEAOE^=BOE^ (hai góc tương ứng)
Hay OE là phân giác của góc xOy.