Cho tam giác ABC có A H ⊥ B C và B A H ^ = 2. C ^ . Tia phân giác của góc B cắt AC tại E. Tia phân giác của góc BAH cắt BE ở I. Khi đó tam giác AIE là tam giác
A. Vuông cân tại I
B. Vuông cân tại E
C. Vuông cân tại A
D. Cân tại I
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
8 tháng 12 2019
Đúng(0)
Những câu hỏi liên quan
2 tháng 2 2018
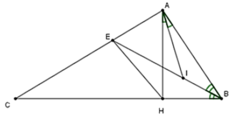
Ta có: AH vuông góc BC suy ra hình tam giác AHC vuông tại H, hình tam giác AHB vuông tại H
\(=>\) \(\widehat{C}+\widehat{HAC}=90^o\) ; \(\widehat{ABH}+\widehat{BAH}=90^o\)
Có: AI là phân giác \(\widehat{BAH}\)nên \(\widehat{IAH}\)= \(\widehat{IAB}=\frac{1}{2}\widehat{BAH}=\widehat{C}\)[ vì theo giả thiết có \(\widehat{BAH}=2\widehat{C}\)]
Suy ra \(\widehat{IAH}+\widehat{HAC}=90^o\)
\(=>\)\(\widehat{IAC}=90^o\)hay \(\widehat{IAE}=90^o=>\Delta IAE\)vuông tại A [1]
Lại có \(\widehat{AIE}=\widehat{IAB}+\widehat{IBA}\)[góc ngoài tại đỉnh I của \(\Delta ABI\)]
Mà BE là phân giác \(\widehat{ABH}\Rightarrow\widehat{IBA}=\frac{1}{2}\widehat{ABH}\)
Suy ra: \(\widehat{AIE}=\frac{1}{2}\left[\widehat{BAH}+\widehat{ABH}\right]=\frac{1}{2}.90^o=45^o\)[2]
Từ 1 và 2 suy ra \(\Delta AIE\)vuông cân tại A
Suy ra AE là phân giác ngoài của \(\Delta ABH\)tại A,BE là phân giác trong tại B của \(\Delta ABH\)
=> HE là phân giác ngoài tại H của \(\Delta BAH\)
=> HE là phân giác \(\widehat{AHC}\)
Vậy ta có điều phải chứng minh
8 tháng 1 2019
a có: AH vuông góc BC suy ra hình tam giác AHC vuông tại H, hình tam giác AHB vuông tại H
=> \widehat{C}+\widehat{HAC}=90^o ; \widehat{ABH}+\widehat{BAH}=90^o Có: AI là phân giác \widehat{BAH}nên \widehat{IAH}= \widehat{IAB}=\frac{1}{2}\widehat{BAH}=\widehat{C}
[ vì theo giả thiết có \widehat{BAH}=2\widehat{C}BAH=2C]
Suy ra \widehat{IAH}+\widehat{HAC}=90^o =>\widehat{IAC}=90^o hay \widehat{IAE}=90^o=>\Delta IAE=>ΔIAEvuông tại A [1]
Lại có \widehat{AIE}=\widehat{IAB}+\widehat{IBA}A[góc ngoài tại đỉnh I của \Delta ABIΔABI]
Mà BE là phân giác \widehat{ABH}\Rightarrow\widehat{IBA}=\frac{1}{2}\widehat{ABH}ABH
Suy ra: \widehat{AIE}=\frac{1}{2}\left[\widehat{BAH}+\widehat{ABH}\right]=\frac{1}{2}.90^o=45^oA[2]
Từ 1 và 2 suy ra \Delta AIE vuông cân tại A
Suy ra AE là phân giác ngoài của \Delta ABH tại A,BE là phân giác trong tại B của \Delta ABH
=> HE là phân giác ngoài tại H của \Delta BAH
=> HE là phân giác \widehat{AHC}
Vậy ta có điều phải chứng minh
8 tháng 4 2019
\(\Delta ABC\)có đường cao AH(gt) => Góc AHB = 90 độ
Xét tam giác AHB vuông tại H có
Góc BAH + góc ABh = 90 độ( do góc ABH = 90 độ
=> góc BAI + góc ABI = 45 độ
Có I nằm giữa B và F => Góc AIF là góc ngoài của tam giác BIA
=> góc AIF= góc ABI+ góc IAB= 45 độ (1)
Có góc BAH = 2 (góc C)
=> góc IAH= góc C
Ta lại có : góc FBC + góc IAH =45 độ
=> góc FBC + góc C =45 độ
=> góc AFI= 45 độ ( là góc ngoài của tam giác FBC) (2)
Từ (1) và (2) => tam giác AIF cân tại A(*)
Xét tam giác AIF có
góc AIF+ góc AFI + góc FAI=180 độ
=> góc IAF =90 độ(**)
Từ *) và (**) => tam giác AIFvuông cân tại A
8 tháng 4 2019
https://olm.vn/hoi-dap/detail/5819899271.html