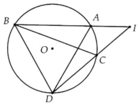
Cho đường tròn (O) và điểm I nằm ngoài (O). Từ điểm I kẻ hai dây cung AB và CD (A nằm giữa I và B, C nằm giữa I và D). Tích IA.IB bằng
A. ID.CD
B. IC.CB
C. IC.CD
D. IC.ID
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
11 tháng 2 2023
a) So sánh \(\widehat{ACI}\) và \(\widehat{ABD}\) và cặp góc \(\widehat{CAI}\) và \(\widehat{CDB}\)
Ta có \(\widehat{ACI}+\widehat{ACD}=180^o\) (hai góc kề bù) \(\left(1\right)\)
Xét \(\left(O\right)\) có:
\(\widehat{ABD}\) là góc nối tiếp chắn cung \(AD\)
\(\widehat{ACD}\) là góc nối tiếp chắn cung \(AD\)
\(\Rightarrow\widehat{ABD}+\widehat{ACD}=\dfrac{1}{2}.360^o=180^o\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ⇔ \(\widehat{ACI}=\widehat{ABD}=180^o-\widehat{ACD}\)
Ta có: \(\widehat{CAI}+\widehat{BAC}=180^o\) (hai góc kề bù)
Xét \(\left(O\right)\) có:
\(\widehat{BAC}\) là góc nội tiếp của chắn cung \(BC\)
\(\widehat{CDB}\) là góc nội tiếp của chắn cung \(BC\)
\(\Rightarrow\widehat{BAC}+\widehat{CDB}=\dfrac{1}{2}.360^o=180^o\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\widehat{CAI}=\widehat{CDB}=180^o-\widehat{BAC}\)
b) Chứng minh tam giác IAC đồng dạng với tam giác IDB
Xét \(\Delta IAC\) và \(\Delta IDB\) có:
\(\widehat{A}\) là góc chung
\(\widehat{IAC}=\widehat{IDB}\) (câu a)
\(\Rightarrow\Delta IAC\sim\Delta IDB\)
c) Chứng minh \(IA.IB=IC.ID\)
Theo câu b ta có \(\Delta IAC\sim\Delta IDB\)
Suy ra: \(\dfrac{IA}{ID}=\dfrac{IC}{IB}\)
Hay: \(IA.IB=IC.ID\) (đpcm)
11 tháng 2 2023
a: ACDB là tứ giác nội tiếp
=>góc ABD+góc ACD=180 độ;góc BAC+góc BDC=180 độ
=>góc ACI=góc ABD;góc CAI=góc CDB
b: Xét ΔIAC và ΔIDB có
góc IAC=góc IDB
góc AIC chung
=>ΔIAC đồng dạg với ΔIDB
c: ΔIAC đồng dạng vơi ΔIDB
=>IA/ID=IC/IB
=>IA*IB=IC*ID
CM
1 tháng 4 2019
a, HS tự chứng minh
b, ∆IAC:∆IDB (g.g)
c, Sử dụng kết quả câu b)
CM
16 tháng 10 2018
a, M C D ^ = B I D ^ = 1 2 s đ C D ⏜
b, Sử dụng kết quả câu a)
Chọn đáp án D