Tìm giá trị của a và b để hai đường thẳng ( d 1 ) ∶(3a - 1)x + 2by = 56 và ( d 2 :1/2 ax - (3b + 2)y = 3 cắt nhau tại điểm M(2; -5).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo đề, ta có:
\(\left\{{}\begin{matrix}2\left(3a-1\right)-10b=56\\\dfrac{1}{2}\cdot a\cdot2+5\left(3b-2\right)=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6a-10b=58\\a+15b=13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6a-10b=58\\6a+90b=78\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{1}{5}\\a=10\end{matrix}\right.\)

Hai đường thẳng:
(
d
1
): (3a – 1)x + 2by = 56 và (
d
2
):
1
2
a
x
-
3
b
+
2
y
=
3
cắt nhau tại điểm M(2; -5) nên tọa độ của M là nghiệm của hệ phương trình: 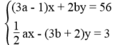
Thay x = 2, y = -5 vào hệ phương trình, ta có:
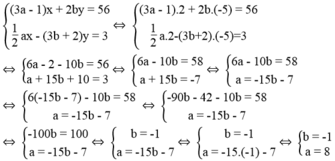
Vậy khi a = 8, b = -1 thì hai đường thẳng (d1): (3a – 1)x + 2by = 56 và (d2): 1 2 a x - 3 b + 2 y = 3 cắt nhau tại điểm M(2; -5).

Hai đường thẳng:
(d1): (3a – 1)x + 2by = 56 và (d2): 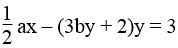
Thay x = 2, y = -5 vào hệ phương trình, ta có:
Vậy khi a = 8, b = -1 thì hai đường thẳng (d1): (3a – 1)x + 2by = 56 và (d2): 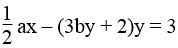
\((3a-1)x+2by=56(A:3a-1;B:2b)\)(d1)
\(\frac{1}{2}ax-\left(3b+2\right)y=3\left(A:\frac{1}{2}a;B:3b+2\right)\)(d2)
Hai đường thẳng cắt tại điểm M (2;-5) tức là\(x=2,y=-5\) ta thay \(x=2,y=-5\) vào (d1, d2), ta có:
(d1) \(\left(3a-1\right).2+2b.\left(-5\right)=56\\ \Leftrightarrow6a-2-10b=56\\ \Leftrightarrow6a-10b=56+2\\ \Leftrightarrow6a-10b=58\left(1\right)\)
(d2) \(\frac{1}{2}a.2-\left(3b+2\right)\left(-5\right)=3\\ \Leftrightarrow a+15b+10=3\\ \Leftrightarrow a+15b=3-10\\ \Leftrightarrow a+15b=-7\left(2\right)\)
Từ (1) và (2), ta có hệ pt:
\(\left\{{}\begin{matrix}6a-10b=58\\a+15b=-7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}6a-10b=58\\6a+90b=-42\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}90b-\left(-10\right)b=-42-58\\a+15b=-7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}100b=-100\\a+15b=-7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=-1\\a+15.\left(-1\right)=-7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=-1\\a-15=-7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=-1\\a=-7+15=8\end{matrix}\right.\)
Vậy giá trị của a và b khi d1, d2 cắt tại M(2;-5) là \(a=8;b=-1\)

Để hai đường cắt nhau trên trục tung thì n+5=1 và m-3<>-2
=>n=-4 và m<>1
Để hai đường cắt nhau trên trục tung thì n+5=1 và m-3<>-2
=>n=-4 và m<>1
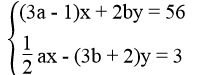
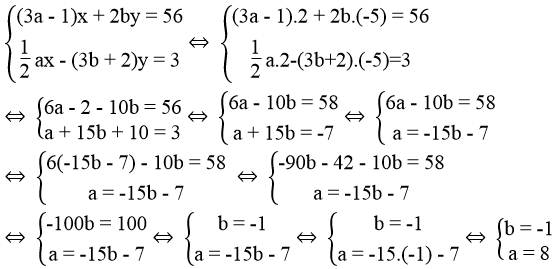
Hai đường thẳng ( d 1 ) và ( d 2 ) cắt nhau tại M(2; -5) nên:
M ∈ ( d 1 ): 3 a - 1 2 + 2b.(-5) = 56 ⇔ 6a - 10b = 58
M ∈ ( d 2 ): 1/2 a.2 - (3b + 2)(-5) = 3 ⇔ a + 15b = -7Khi đó, ta có hệ phương trình:
Vậy a = 8 và b = -1 thì hai đường thẳng ( d 1 ) và ( d 2 ) cắt nhau tại M(2; -5).