Tứ giác ở hình nào dưới đây là tứ giác nội tiếp?
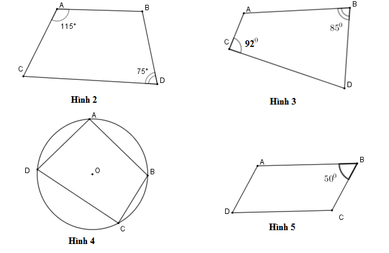
A. Hình 2
B. Hình 3
C. Hình 4
D. Hình 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
19 tháng 2 2018
Chọn đáp án C
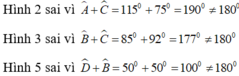
Hình 4 đúng vì tứ giác này có 4 đỉnh cùng thuộc một đường tròn
VT
0
PT
1
CM
1 tháng 9 2018
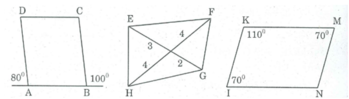
* Tứ giác ABCD là hình bình hành vì AB // CD và AB = CD.
* Tứ giác IKMN có: ∠ I + ∠ K + ∠ N + ∠ M = 360 0
Suy ra: ∠ N = 360 0 - ( ∠ K + ∠ I + ∠ M) = 110 0
Ta có ∠ I = ∠ M = 70 0 và ∠ K = ∠ N = 110 0
Suy ra IKMN là hình bình hành (tứ giác có các góc đối bằng nhau).
* Tứ giác EFGH không là hình bình hành vì có hai đường chéo không cắt nhau tại trung điểm mỗi đường.
16 tháng 4 2021
b) Xét ΔFDC có
A\(\in\)FD(gt)
B\(\in\)FC(gt)
AB//CD(gt)
Do đó: \(\dfrac{FA}{AD}=\dfrac{FB}{BC}\)(Định lí Ta lét)
\(\Leftrightarrow\dfrac{FA}{FB}=\dfrac{AD}{BC}=1\)
hay FA=FB
Ta có: FA+AD=FD(A nằm giữa F và D)
FB+BC=FC(B nằm giữa F và C)
mà FA=FB(cmt)
và AD=BC(ABCD là hình thang cân)
nên FD=FC
Ta có: FA=FB(cmt)
FD=FC(cmt)
Do đó: \(FA\cdot FD=FB\cdot FC\)(đpcm)
16 tháng 4 2021
a) Ta có: ABCD là tứ giác nội tiếp(gt)
nên \(\widehat{A}+\widehat{C}=180^0\)(hai góc đối)(1)
Ta có: ABCD là hình thang(AB//CD)
nên \(\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)(2)
Từ (1) và (2) suy ra \(\widehat{C}=\widehat{D}\)
Hình thang ABCD(AB//CD) có \(\widehat{C}=\widehat{D}\)(cmt)
nên ABCD là hình thang cân(Dấu hiệu nhận biết hình thang cân)
CM
3 tháng 6 2017
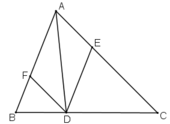
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).
Chọn đáp án C
Hình 4 đúng vì tứ giác này có 4 đỉnh cùng thuộc một đường tròn