Cho nửa đường tròn tâm O, đường kính AB. Dựng các tiếp tuyến Ax và By với đường tròn. Lấy điểm I bất kì trên nửa đường tròn, tiếp tuyến tại I cắt Ax, By lần lượt tại C và D. Khẳng định nào sau đây là sai?
A. AC + BD = CD B. AC . BD =
R
2
C.
O
D
2
= DB. (AC + DB) D. Có 2 khẳng định...
Đọc tiếp
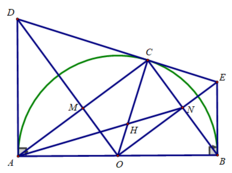
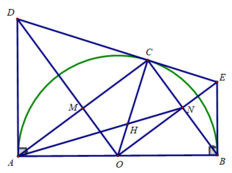
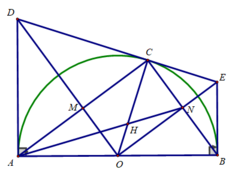
Cho nửa đường tròn tâm O, đường kính AB. Dựng các tiếp tuyến Ax và By với đường tròn. Lấy điểm I bất kì trên nửa đường tròn, tiếp tuyến tại I cắt Ax, By lần lượt tại C và D. Khẳng định nào sau đây là sai?
A. AC + BD = CD
B. AC . BD = R 2
C. O D 2 = DB. (AC + DB)
D. Có 2 khẳng định sai
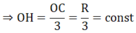
Đáp án D
* Do AC và CI là 2 tiếp tuyến cắt nhau tại C nên: CA = CI ( tính chất 2 tiếp tuyến cắt nhau)
* Do BD và DI là 2 tiếp tuyến cắt nhau tại D nên: DB = DI ( tính chất 2 tiếp tuyến cắt nhau).
Suy ra: AC + BD = CI + DI = CD.
+) AC.BD = CI.DI (1)
Xét tam giác COD vuông tại O có đường cao OI nên:
CI.ID = I O 2 = R 2 (2)
Từ (1) và (2) suy ra: AC.BD = R 2
Và O D 2 = DI.DC = DB . (AC + BD)