Cho tam giác ABC nhọn biết 3 góc của tam giác lập thành một cấp số cộng ; số đo góc A nhỏ nhất và sin A = 2 2 .Tìm các góc của tam giác?
A. 60º; 75º
B. 75º; 80º
C. 50º; 85º
D. 55º; 80º
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Gọi số đo ba góc ba góc lập thành cấp số cộng là 25; 25+ d ; 25 +2d có công sai d.
Tổng ba góc trong một tam giác bằng 1800 nên :
u 1 + u 2 + u 3 = 180 ⇔ 25 + 25 + d + 25 + 2 d = 180 ⇔ 3 d = 105 ⇔ d = 35 .
Vâỵ
u 2 = 25 + 35 = 60 ; u 3 = 25 + 2 . 35 = 95.

Gọi 3 góc lần lượt là \(a;b;90\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=90\\2b=a+90\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=30\\b=60\end{matrix}\right.\)
Vậy số đo 3 góc là \(30^0;60^0;90^0\)

Do tam giác đó là tam giác vuông nên có một góc bằng \({90^ \circ }\).
Giả sử hai góc còn lại của tam giác có số đo lần lượt là \(a,b\left( {{0^ \circ } < a,b < {{90}^ \circ }} \right)\).
Vì tổng ba góc trong tam giác bằng \({180^ \circ }\) nên ta có: \(a + b + {90^ \circ } = {180^ \circ } \Leftrightarrow a + b = {90^ \circ }\)(1).
Vì số đo ba góc trong tam giác lập thành cấp số cộng nên ta có:
\(b = \frac{{a + {{90}^ \circ }}}{2} \Leftrightarrow 2b = a + {90^ \circ } \Leftrightarrow - a + 2b = {90^ \circ }\) (2)
Từ (1) và (2) ta có hệ phương trình sau:
\(\left\{ \begin{array}{l}a + b = {90^ \circ }\\ - a + 2b = {90^ \circ }\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = {30^ \circ }\\b = {60^ \circ }\end{array} \right.\)
Vậy số đo ba góc của tam giác vuông đó lần lượt là: \({30^ \circ };{60^ \circ };{90^ \circ }\).

Chọn C
Giả sử ba cạnh của tam giác ABC là a,b,c. u 1 + u 1 q 4 = 51
không mất tính tổng quát, ta giả sử 0 < a≤a≤b≤c, nếu chúng tạo thành cấp số nhân thì theo tính chất của cấp số nhân Ta có: b2=ac.
Theo định lý hàm côsin Ta có:
![]()
![]()
Mặt khác a 2 + c 2 ≥ 2 a c ⇒ cos B ≥ 1 − 1 2
Vậy góc B ^ ≤ 60 ° ,mà a ≤ b ⇒ A ≤ 60 ° , cho nên tam giác ABC có hai góc không quá 60°

Giả sử 3 cạnh của tam giác ABC theo thứ tự a, b, c. Không giảm tính tổng quát, ta giả sử 0 < a \(\le b\le c\), nếu chúng tạo thành cấp số nhân thì, theo tính chất của cấp số nhân ta có : \(b^2=ac\)
Theo định lí hàm số côsin, ta có :
\(b^2=a^2+c^2-2ac\cos B\Rightarrow ac=a^2+c^2-2ac.\cos B\)
\(\Leftrightarrow\cos B=\frac{a^2+c^2}{2ac}-\frac{1}{2}\)
Mặt khác \(a^2+c^2\ge2ac\Rightarrow\cos B\ge1-\frac{1}{2}=\frac{1}{2}\)
Vậy góc \(B\le60^0\)
Nhưng \(a\le b\Rightarrow A\le60^0\) cho nên tam giác ABC có 2 góc không quá \(60^0\)

Chọn D
Theo tính chất cấp số nhân, Ta có: ac=2/3 b2. Theo hệ thức lượng trong tam giác vuông, Ta có: b=a.sinB, c=a.cosB. vậy Ta có
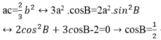
![]()
Chọn A.
Ta có và tam giác ABC nhọn nên A = 45º.
và tam giác ABC nhọn nên A = 45º.
A + B + C = 180 º ⇒ B + C = 180º - 45º = 135º
Do 3 góc tam giác lập thành cấp số cộng ; số đo góc A nhỏ nhất nên B = A + d; C = A + 2d.
Khi đó: B + C = A + d + A + 2d = 2A + 3d ⇒ 3d = 135º - 2.45º = 45º
⇒ d = 15º ⇒ B = A + d = 60º; C = A + 2d = 75º