Tìm x,y,z biết rằng:
y+z+1/x=z+x+2/y=x+y-3/z=1/x+y+z
(giải lun hộ mk nha)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
HG
0
NT
0
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
\(\dfrac{x}{y+z+1}\) = \(\dfrac{y}{x+z+2}\) = \(\dfrac{z}{x+y-3}\) = \(x+y+z\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{y+z+1}\)=\(\dfrac{y}{x+z+2}\)=\(\dfrac{z}{x+y-3}\)=\(\dfrac{x+y+z}{y+z+1+x+z+2+x+y-3}\)
\(x+y+z\) = \(\dfrac{x+y+z}{2.\left(x+y+z\right)}\) = \(\dfrac{1}{2}\) (1)
\(\dfrac{x}{y+z+1}\) = \(\dfrac{1}{2}\) ⇒ 2\(x\) = y+z+1
⇒ 2\(x\) + \(x\) = \(x+y+z+1\) (2)
Thay (1) vào (2) ta có: 2\(x\) + \(x\) = \(\dfrac{1}{2}\) + 1
3\(x\) = \(\dfrac{3}{2}\) ⇒ \(x=\dfrac{1}{2}\)
\(\dfrac{y}{x+z+2}\) = \(\dfrac{1}{2}\) ⇒ 2y = \(x+z+2\) ⇒ 2y+y = \(x+y+z+2\) (3)
Thay (1) vào (3) ta có: 2y + y = \(\dfrac{1}{2}\) + 2
3y = \(\dfrac{5}{2}\) ⇒ y = \(\dfrac{5}{6}\)
Thay \(x=\dfrac{1}{2};y=\dfrac{5}{6}\) vào (1) ta có: \(\dfrac{1}{2}+\dfrac{5}{6}+z\) = \(\dfrac{1}{2}\)
\(\dfrac{5}{6}\) + z = 0 ⇒ z = - \(\dfrac{5}{6}\)
Kết luận: (\(x;y;z\)) = (\(\dfrac{1}{2}\); \(\dfrac{5}{6}\); - \(\dfrac{5}{6}\))
16 tháng 8 2023
TH1: x + y + z 0
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
= = =
= = =
⇒ x + y + z =
⇒ x + y = - z
x + z = - y
y + z = - x
Thay y + z + 1 = - x + 1
⇒ =
⇒ 2x = - x + 1
⇒ 2x + x = + 1
⇒ 3x =
⇒ x =
Thay x + z + 2 = - y + 2
⇒ =
⇒ 2y = - y + 2
⇒ 2y + y = + 2
⇒ 3y =
⇒ y =
Thay x + y - 3 = - z - 3
⇒ \frac{1}{2}$
⇒ 2z = - z - 3
⇒ 2z + z = - 3
⇒ 3z =
⇒ z =
TH2: x + y + z = 0
⇒ = = = 0
⇒ x = y = z = 0
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
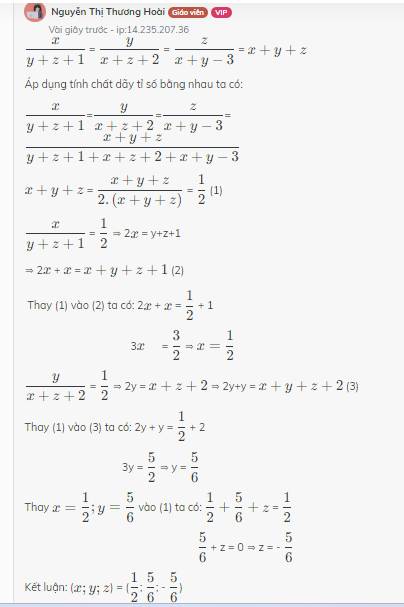
https://olm.vn/cau-hoi/tim-tat-ca-cac-so-xyz-biet-dfracxyz1dfracyxz2dfraczxy-3xyz-giair-chi-tiet-ho-e-vs-a.8297156371934
12 tháng 8 2018
Vậy theo đề của mình nhé !
* trước tiên ta xét trường hợp x + y + z = 0, ta có :
\(\dfrac{x}{y+z+1}=\dfrac{y}{x+z+2}=\dfrac{z}{x+y-3}=0\Rightarrow x=y=z=0\)
* xét x + y + z ≠ 0, ta có :
Áp dụng t/c dãy tỉ số bằng nhau, ta có :
\(\dfrac{x}{y+z+1}=\dfrac{y}{x+z+2}=\dfrac{x}{x+y-3}=\dfrac{x+y+z}{y+z+x+z+x+y}=\)
\(\dfrac{x+y+z}{2\left(x+y+z\right)}=\dfrac{1}{2}=x+y+z\)
⇒ x + y + z = 1/2 và:
+ 2x = y + z + 1 = 1/2 - x + 1 ⇒ x = 1/2
+ 2y = x + z + 2 = 1/2 - y + 2 ⇒ y = 1/2
+ z = 1/2 - (x + y) = 1/2 - 1 = -1/2
Vậy có cặp (x,y,z) thỏa mãn là : (0, 0, 0) và (1/2,1/2,-1/2)
MN
4
4 tháng 1 2016
Áp dụng ...............ta có :
x/z+y+1=y/x+z+1=z/x+y-2=1/2
+,x/z+y+1=1/2=>2x=z+y+1
=>2x-1=z+y
lại có x+y+z=1/2(1)=>x+2x-1=1/2
=>3x=1/2+1=3/2
=>x=3/2 /3=1/2
+,y/x+z+1=1/2=>2y=x+z+1
=>2y-1=x+z
Từ 1 =>2y-1+y=x+y+z
=>3y=1/2+1=3/2
=>y=3/2 /2 = 1/2
Thãy=1/2;y=1/2 vào 1 ta có :
1/2+1/2+z=1/2
z=1/2-1/2-1/2=-1/2