Cho đường tròn (O), điểm A nằm bên trong đường tròn. Vẽ dây BC vuông góc với OA tại A. Vẽ dây EF bất kì đi qua A và không vuông góc với OA. Hãy so sánh độ dài hai dây BC và EF.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 8 2017
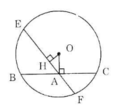
Kẻ OH ⊥ EF.
Trong tam giác vuông OHA vuông tại H có OA > OH (đường vuông góc ngắn hơn đường xiên).
Vì OA > OH nên BC < EF (định lí 3).
25 tháng 4 2017
Vẽ OH⊥EFOH⊥EF.
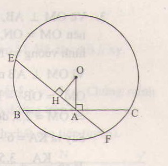
Xét tam giác HOA vuông tại H ta có OH<OA
Suy ra EF>BC..
Nhận xét. Trong các dây đi qua một điểm A ở trong đường tròn, dây vuông góc với OA là dây ngắn nhất.
2 tháng 1 2022
b: \(AB=3\sqrt{3}\left(cm\right)\)
Xét ΔOAB vuông tại B có
\(\sin\widehat{AOB}=\dfrac{AB}{AO}=\dfrac{3\sqrt{3}}{6}=\dfrac{\sqrt{3}}{2}\)
hay \(\widehat{AOB}=60^0\)
AH
Akai Haruma
Giáo viên
30 tháng 12 2020
Lời giải:
Đề bài cần bổ sung OA cắt (O) tại E sao cho E nằm giữa O và A.
Do $AB$ là tiếp tuyến $(O)$ nên $AB\perp OB$ hay tam giác $ABO$ vuông tại $B$. Mà $AB=2BO$ (do $AB=2R; BO=R$). Do đó $\widehat{BOA}=60^0$
Tam giác $BOE$ có $BO=EO=R$ nên là tam giác cân. Mà $\widehat{BOE}=\widehat{BOA}=60^0$ nên $BOE$ là tam giác đều.
$\Rightarrow BO=BE(1)$$OB=OC$ và $OA\perp BC$ nên $OA$ là đường trung trực của $BC$
$E\in OA$ nên $EB=EC(2)$
$OB=OC=R(3)$
Từ $(1);(2);(3)\Rightarrow OC=BO=BE=EC$. Suy ra OBEC là hình thoi.
17 tháng 11 2023
a: BA là tiếp tuyến của (O) có B là tiếp điểm
=>OB\(\perp\)BA tại B
=>ΔOBA vuông tại B
ΔBOA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(BA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(BA=R\sqrt{3}\)
b: ΔOBC cân tại O
mà OA là đường cao
nên OA là tia phân giác của \(\widehat{BOC}\)
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OCA}=\widehat{OBA}=90^0\)
=>AC là tiếp tuyến của (O)
c: Xét ΔABO vuông tại B có \(sinBAO=\dfrac{BO}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BAO}=30^0\)
ΔOBA=ΔOCA
=>\(\widehat{BAO}=\widehat{CAO}\) và AB=AC
=>\(\widehat{BAC}=2\cdot\widehat{BAO}=2\cdot30^0=60^0\)
Xét ΔABC có AB=AC và \(\widehat{BAC}=60^0\)
nên ΔABC đều
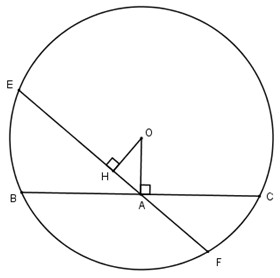
Kẻ OH ⊥ EF.
Trong tam giác vuông OHA vuông tại H có OA > OH (đường vuông góc ngắn hơn đường xiên).
Vì OA > OH nên BC < EF (định lí 3).