Giải các bất phương trình:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)

1) \(ĐK:x\ne2\)
Nếu \(x>2\)
BPT ⇔ \(x^2-2x+5-\left(x-1\right)\left(x-2\right)\ge0\) ⇔ \(x^2-2x+5-\left(x^2-3x+3\right)\ge0\)
⇔\(x+2\ge0\) ⇔\(x\ge-2\) ⇒ Lấy \(x\ge2\)
Nếu \(x< 2\)
BPT ⇔\(\dfrac{-\left(x^2-2x+5\right)}{x-2}-x+1\ge0\) ⇔\(-x^2+2x-5-\left(x-1\right)\left(x-2\right)\ge0\)
⇔\(-x^2+2x-5-x^2+3x-2\ge0\)
⇔\(-2x^2+5x-7\ge0\)
⇔\(x^2-\dfrac{5}{2}x+\dfrac{7}{2}\le0\)
⇔\(\left(x-\dfrac{5}{4}\right)^2\le\dfrac{11}{4}\)
⇔\(\left[{}\begin{matrix}x-\dfrac{5}{4}\le\dfrac{11}{4}\\x-\dfrac{5}{4}\le\dfrac{-11}{4}\end{matrix}\right.\) ⇔\(\left[{}\begin{matrix}x\le4\\x\le\dfrac{-3}{2}\end{matrix}\right.\) ⇔ \(x\le\dfrac{-3}{2}\)
S= [2;+∞)U(-∞;\(\dfrac{-3}{2}\)]
2) \(ĐK:x\ne-1\)
Nếu \(x>-1\)
BPT ⇔ \(2x-3-2\left(x+1\right)< 0\) ⇔\(2x-3-2x-2< 0\)
⇔\(-5< 0\) ( luôn đúng với mọi \(x>-1\))
Nếu \(x< -1\)
BPT⇔\(\dfrac{-\left(2x-3\right)}{x+1}-2< 0\) ⇔\(-\left(2x-3\right)-2\left(x+1\right)< 0\) ⇔\(-4x+1< 0\) ⇔ \(x>\dfrac{-1}{4}\)
Vậy S=....

1.
$2(-2x+1)\leq -x+3$
$\Leftrightarrow -4x+2\leq -x+3$
$\Leftrightarrow -1\leq 3x$
$\Leftrightarrow x\geq \frac{-1}{3}$
2.
$2(x+1)\leq -x+3$
$\Leftrightarrow 2x+2\leq -x+3$
$\Leftrightarrow 3x\leq 1$
$\Leftrightarrow x\leq \frac{1}{3}$
3.
$5-3(x-1)>2$
$\Leftrightarrow 5-(3x-3)>2$
$\Leftrightarrow 8-3x>2$
$\Leftrightarrow 8-3x-2>0$
$\Leftrightarrow 6-3x>0$
$\Leftrightarrow 6>3x$
$\Leftrightarrow x< 2$
4.
$x^2-12x+3-(x-3)^2>0$
$\Leftrightarrow x^2-12x+3-(x^2-6x+9)>0$
$\Leftrightarrow -6x-6>0$
$\Leftrightarrow -6>6x$
$\Leftrightarrow x< -1$

a: Ta có: \(3x-5\ge2\left(x-6\right)-12\)
\(\Leftrightarrow3x-5\ge2x-24\)
hay \(x\ge-19\)
b: Ta có: \(2\left(5-2x\right)\ge3-x\)
\(\Leftrightarrow10-4x-3+x\ge0\)
\(\Leftrightarrow-3x\ge-7\)
hay \(x\le\dfrac{7}{3}\)

\(a,\left(\dfrac{1}{3}\right)^{2x+1}\le9\\ \Leftrightarrow2x+1\ge-2\\ \Leftrightarrow2x\ge-3\\ \Leftrightarrow x\ge-\dfrac{3}{2}\)
\(b,4^x>2^{x-2}\\ \Leftrightarrow2^{2x}>2^{x-2}\\ \Leftrightarrow2x>x-2\\ \Leftrightarrow x>-2\)
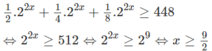
Vậy bất phương trình có tập nghiệm