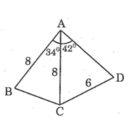
Cho hình bên. Biết AB = AC = 8cm, CD = 6cm, ∠ BAC = 34 ° và ∠ CAD = 42 °
Hãy tính: Độ dài cạnh BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
18 tháng 4 2019
Đúng(0)
Những câu hỏi liên quan
+Cho+hình+biết:+AB=AC=8cm,CD=6cm,+góc+BAC=34+độ+và+góc+CAD=42+độ.Hãy+tính:+A)+Độ+dài+cạnh+BC+B)+góc+ADC+C)+Kh...){kind=link}
TT
13 tháng 5 2018
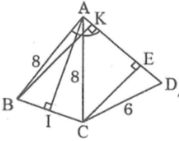
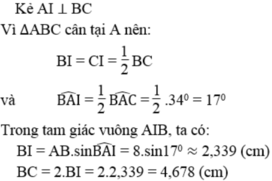
a) Kẻ AM vuong goc voi BC tai M
Tam giac BAC can tai A, co AM la duong cao=> AM cung la trung tuyen va phan giac cua tam giac ABC => MB=MC va goc BAM = goc CAM = 34/2=17 do
Xet tam giac AMB vuong tai M, ta co:
sin BAM = BM/AB => BM = AB.sinBAM = 8.sin(17 do)
Suy ra BC= 2.BM = 16.sin(17 do)
b) Ve CH vuong goc voi AD tai H
Xet tam giac AHC vuong tai H co:
sinCAD = CH/AC => CH= AC.sinCAD=8.sin(42 do)
Xet tam giac CHD vuong tai H co:
sin ADC = CH/CD = 8.sin(42 do)/6 => goc ADC = ( bam may tinh)
c) Ve BK vuong goc voi AD tai K( K nam giua A,D), nhu vay khoang cach tu B den AD chinh la BK
goc BAD= goc BAC + goc CAD = 34 +42 = 76 do
Xet tam giac AKB vuong tai K, ta co:
sinBAD = BK./AB => BK =AB. sinBAD = 8.sin(72 do)
AN
13 tháng 5 2018
a)Kẻ đường cao AH
Ta có AB = AC => tam giác ABC cân tại A
Nên đường cao AH vừa là phân giác, vừa là trung trực
Suy ra BAHˆBAH^ = CAHˆCAH^ = BACˆ2BAC^2 = 34023402 = 170170
Xét tam giác AHC vuông tại H, ta có:
sin CAHˆCAH^ = HCACHCAC => HC = sin CAHˆCAH^.AC = sin 170170.8 = 2,34
Do AH là trung trực của tam giác ABC nên BC = 2HC = 2.2,34 = 4,68
Vậy BC = 4,68cm
b) Kẻ CE vuông góc với AD
Xét tam giác ACE vuông tại E, ta có:
ADEˆADE^ = CEACCEAC => CE = sin CAEˆCAE^.AC = sin 420ˆ420^.8 = 5,353
Xét tam giác CED vuông tại E, ta có
sin CDEˆCDE^ = CECDCECD = 5,35365,3536 ≈≈ 0,8922
Suy ra CDEˆCDE^ = 63,15063,150 = 6306309'
Hay ADCˆADC^ = 63,15063,150
c) Ta có BADˆBAD^ = BACˆBAC^ + CADˆCAD^ = 340340 + 420420 = 760760
Kẻ BF vuông góc với AD
Xét tam giác BFA vuông tại F, ta có
BF = sin BADˆBAD^.AB = sin 760760.8 = 7,76
Vậy khoảng cách từ điểm B đến cạnh AD bằng 7,76cm