Tìm giá trị lớn nhất của hàm số: y = 3 - 2sinx
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)

\(-1\le sinx\le1\Rightarrow2.\left(-1\right)-4\le y\le2.1-4\)
\(\Rightarrow-6\le y\le-2\)
\(y_{min}=-6\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=1\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)

Đặt \(sinx=t\in\left[-1;1\right]\)
\(y=f\left(t\right)=t^2+2t\)
Xét hàm \(y=f\left(t\right)=t^2+2t\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=-1\in\left[-1;1\right]\)
\(f\left(-1\right)=-1\) ; \(f\left(1\right)=3\)
\(\Rightarrow y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)

Đáp án B
Điều kiện 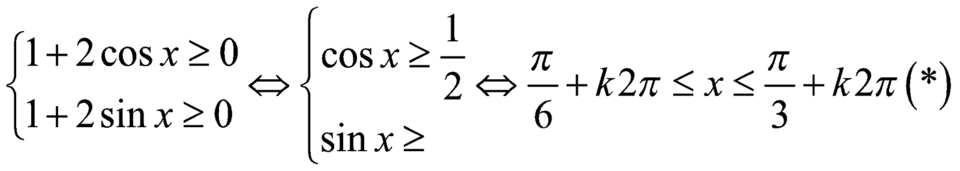
Theo bất đẳng thức BunhiaCopxki: ![]()
![]()
Dấu bằng xảy ra khi và chỉ khi ![]() (thỏa mãn (*))
(thỏa mãn (*))

f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 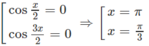
Ta có: f(0) = 0,
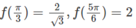
Từ đó ta có: min f(x) = −2 ; max f(x) = 3 3 /2

Chọn A
![]()
↔ (2-y)sinx + (1+2y)cosx= 3y-1(*)
Sử dụng điều kiện để phương trình (*) có nghiệm suy ra -1/2 ≤ y ≤ 2
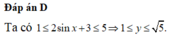

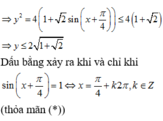
Ta có: -1 ≤ sin x ≤ 1
⇒ -2 ≤ -2sin x ≤ 2
⇒ 1 ≤ 3 – 2sin x ≤ 5
hay 1 ≤ y ≤ 5.
Vậy hàm số đạt giá trị lớn nhất bằng 5.