Giải các hệ phương trình sau: 3 x + y + 9 = 2 x - y 2 x + y = 3 x - y - 11
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
12 tháng 9 2019
Đúng(0)
Những câu hỏi liên quan
CM
29 tháng 1 2018
Bài toán này có hai cách giải:
Cách 1: Thu gọn từng phương trình ta sẽ thu được phương trình bậc nhất hai ẩn x và y.
Cách 2: Đặt ẩn phụ.
Cách 1:
(hệ số của y bằng nhau nên ta trừ từng vế hai phương trình)
Vậy hệ phương trình có nghiệm duy nhất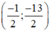 
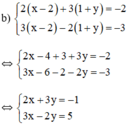
(Nhân hai vế pt 1 với 2; pt 2 với 3 để hệ số của y đối nhau)
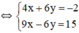(Hệ số của y đối nhau nên ta cộng từng vế của hai pt)
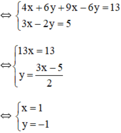
Vậy hệ phương trình có nghiệm duy nhất (1; -1).
Cách 2:
a) Đặt x + y = u và x – y = v (*)
Khi đó hệ phương trình trở thành
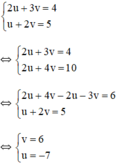
Thay u = -7 và v = 6 vào (*) ta được hệ phương trình:
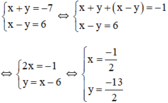
Vậy hệ phương trình có nghiệm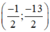 
b) Đặt x – 2 = u và y + 1 = v.
Khi đó hệ phương trình trở thành :
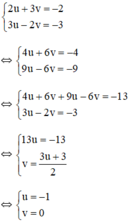
+ u = -1 ⇒ x – 2 = -1 ⇒ x = 1.
+ v = 0 ⇒ y + 1 = 0 ⇒ y = -1.
Vậy hệ phương trình có nghiệm (1; -1).
5 tháng 10 2021
\(a,\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}-\dfrac{2}{y}=2\\\dfrac{2}{x}-\dfrac{3}{y}=5\end{matrix}\right.\left(x,y\ne0\right)\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{5}{y}=3\\\dfrac{2}{x}-\dfrac{3}{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{5}{3}\\\dfrac{2}{x}+\dfrac{9}{5}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{8}\\y=-\dfrac{5}{3}\end{matrix}\right.\)
\(b,\Leftrightarrow\left\{{}\begin{matrix}\dfrac{60}{x}-\dfrac{28}{y}=36\\\dfrac{60}{x}-\dfrac{135}{y}=525\end{matrix}\right.\left(x,y\ne0\right)\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{9}{y}=35\\-\dfrac{163}{y}=489\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}-27=35\\y=-\dfrac{1}{3}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{31}\\y=-\dfrac{1}{3}\end{matrix}\right.\)
5 tháng 10 2021
a: Ta có: \(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=1\\\dfrac{2}{x}-\dfrac{3}{y}=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}-\dfrac{2}{y}=2\\\dfrac{2}{x}-\dfrac{3}{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=-3\\\dfrac{1}{x}-\dfrac{1}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-1}{3}\\\dfrac{1}{x}=1+\dfrac{1}{y}=1+\left(-3\right)=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{1}{3}\\x=\dfrac{-1}{2}\end{matrix}\right.\)
AQ
1
12 tháng 10 2021
\(\left\{{}\begin{matrix}\left(x-5\right)\left(y-2\right)=\left(x+2\right)\left(y-1\right)\\\left(x-4\right)\left(y+7\right)=\left(x-3\right)\left(y+4\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy-2x-5y+10=xy-x+2y-2\\xy+7x-4y-28=xy+4x-3y-12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+7y=12\\3x-y=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x+21y=36\\3x-y=16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}22y=20\\x+7y=12\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{62}{11}\\y=\dfrac{10}{11}\end{matrix}\right.\)
XD
3
5 tháng 3 2022
a, \(\left\{{}\begin{matrix}2x+2y=4\\2x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5y=-5\\x=2-y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=3\end{matrix}\right.\)
b, \(\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}\\x+y=10\end{matrix}\right.\)Theo tc dãy tỉ số bằng nhau
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{x+y}{2+3}=\dfrac{10}{5}=2\Rightarrow x=4;y=6\)
5 tháng 3 2022
a.\(\Leftrightarrow\left\{{}\begin{matrix}3x+3y=6\\2x-3y=9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}5x=15\\2x-3y=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\2.3-3y=9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)
b.\(\Leftrightarrow\left\{{}\begin{matrix}3x=2y\\x+y-10=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x-2y=0\\x+y-10=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x-2y=0\\2x+2y=20\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}5x=20\\3x-2y=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=4\\3.4-2y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=6\end{matrix}\right.\)
DX
1
30 tháng 3 2016
Từ phương trình thứ nhất ta có : \(y=x-2\)
Thay vào phương trình thứ 2, ta được :
\(3^{x^2+x-2}=3^{-2}\)
Do đó
\(x^2+x-2=-2\) nên \(x=0\) hoặc \(x=-1\)
Suy ra \(y=-2\) hoặc \(y=-3\)
Vậy hệ có 2 nghiệm là \(\left(0;-2\right)\) và \(\left(-1;-3\right)\)
NV
25 tháng 3 2023
\(\left\{{}\begin{matrix}x^2+y^2+3=4x\\x^3+12x+y^3=6x^2+9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x^2-4x+4\right)+y^2=1\\\left(x^3-6x^2+12x-8\right)+y^3=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-2\right)^2+y^2=1\\\left(x-2\right)^3+y^3=1\end{matrix}\right.\)
Đặt \(a=x-2;b=y\). Hệ phương trình trở thành:
\(\left\{{}\begin{matrix}a^2+b^2=1\\a^3+b^3=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2ab=\left(a+b\right)^2-1\\\left(a+b\right)\left(a^2+b^2-ab\right)=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2ab=\left(a+b\right)^2-1\\\left(a+b\right)\left(1-\dfrac{\left(a+b\right)^2-1}{2}\right)=1\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\left(a+b\right)\left[3-\left(a+b\right)^2\right]=2\)
\(\Leftrightarrow3\left(a+b\right)-\left(a+b\right)^3=2\)
\(\Leftrightarrow\left(a+b\right)^3-3\left(a+b\right)+2=0\)
\(\Leftrightarrow\left(a+b\right)^3-\left(a+b\right)^2+\left(a+b\right)^2-\left(a+b\right)-2\left(a+b-1\right)=0\)
\(\Leftrightarrow\left(a+b\right)^2\left(a+b-1\right)+\left(a+b\right)\left(a+b-1\right)-2\left(a+b-1\right)=0\)
\(\Leftrightarrow\left(a+b-1\right)\left[\left(a+b\right)^2+\left(a+b\right)-2\right]=0\)
\(\Leftrightarrow\left(a+b-1\right)^2\left(a+b+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=1\\a+b=-2\end{matrix}\right.\)
Với \(\left\{{}\begin{matrix}a+b=1\\a^2+b^2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=1\\\left(a+b\right)^2-2ab=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=1\\ab=0\end{matrix}\right.\)
\(\Rightarrow\left(a;b\right)=\left(0;1\right),\left(1;0\right)\)
\(\Rightarrow\left(x-2;y\right)=\left(0;1\right),\left(1;0\right)\)
\(\Rightarrow\left(x;y\right)=\left(2;1\right),\left(3;0\right)\)
Với \(\left\{{}\begin{matrix}a+b=-2\\a^2+b^2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=-2\\\left(a+b\right)^2-2ab=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=-2=S\\ab=\dfrac{3}{2}=P\end{matrix}\right.\left(2\right)\)
Ta có: \(S^2-4P=\left(-2\right)^2-4.\dfrac{3}{2}=-2< 0\)
\(\Rightarrow\)Không tồn tại số a,b nào thỏa hệ phương trình (2).
Vậy nghiệm (x;y) của hpt đã cho là \(\left(2;1\right),\left(3;0\right)\)
AQ
1
28 tháng 9 2021
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(x+y\right)+3\left(x-y\right)=4\\2\left(x+y\right)+4\left(x-y\right)=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=6\\2\left(x+y\right)+24=10\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x-y=6\\x+y=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=-\dfrac{13}{2}\end{matrix}\right.\)
H
2
XO
18 tháng 12 2022
Ta có x + y + z = 0
<=> (x + y + z)2 = 0
<=> \(x^2+y^2+z^2+2xy+2yz+2zx=0\)
\(\Leftrightarrow xy+yz+zx=-3\) (vì x2 + y2 + z2 = 6)
\(\Leftrightarrow x\left(y+z\right)+yz=-3\)
\(\Leftrightarrow-x^2+yz=-3\Leftrightarrow yz=x^2-3\) (vì x + y + z = 0)
Khi đó \(x^3+y^3+z^3=x^3+(y+z).(y^2+z^2-yz)\)
\(=x^3-x.[6-x^2-(x^2-3)]\)
\(=x^3-x.(9-2x^2)=3x^3-9x=6\)
Ta được \(\Leftrightarrow x^3-3x-2=0\Leftrightarrow(x^3+1)-3(x+1)=0\)
\(\Leftrightarrow(x+1)(x^2-x-2)=0\)
\(\Leftrightarrow\left(x+1\right)^2\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
Với x = -1 ta có hệ \(\left\{{}\begin{matrix}y+z=1\\y^2+z^2=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1-z\\(1-z)^2+z^2=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1-z\\z^2-z-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1-z\\\left[{}\begin{matrix}z=-1\\z=2\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}y=2\\z=-1\end{matrix}\right.\\\left\{{}\begin{matrix}y=-1\\z=2\end{matrix}\right.\end{matrix}\right.\)
Với x = 2 ta có hệ : \(\left\{{}\begin{matrix}y+z=-2\\y^2+z^2=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2-z\\(-2-z)^2+z^2=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2-z\\z^2+2z+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-2-z\\z=-1\end{matrix}\right.\Leftrightarrow y=z=-1\)
Vậy (x;y;z) = (2;-1;-1) ; (-1 ; 2 ; -1) ; (-1 ; -1 ; 2)
LT
0