Cho hình chóp S.ABCD có đáy là tứ giác ABCD. Gọi G 1 và G 2 lần lượt là trọng tâm của các tam giác SBC và SCD
Tìm giao tuyến của mặt phẳng ( A G 1 G 2 ) với các mặt phẳng (ABCD) và (SCD).
Xác định thiết diện của hình chóp với mặt phẳng ( A G 1 G 2 ) .



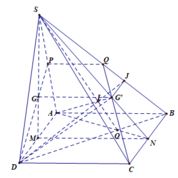






Gọi I, J lần lượt là trung điểm của BC, CD.
Ta có I J / / G 1 G 2 nên giao tuyến của hai mặt phẳng ( A G 1 G 2 ) và (ABCD) là đường thẳng d qua A và song song với IJ
Gọi O = IJ ∩ AC, K = G 1 G 2 ∩ S O , L = AK ∩ SC
L G 2 cắt SD tại R
L G 2 cắt SB tại Q
Ta có thiết diện là tứ giác AQLR.