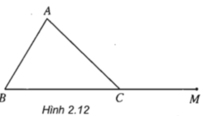
Cho tam giác ABC, M là điểm thuộc phần kéo dài của đoạn thẳng BC (h.2.12). Hãy cho biết M có thuộc mặt phẳng (ABC) không và đường thẳng AM có nằm trong mặt phẳng (ABC) không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

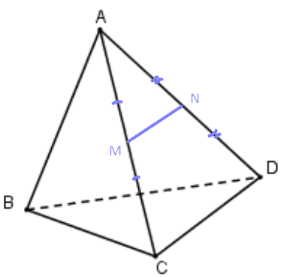
a) Ta có AM cắt (BCD) tại C suy ra AM không song song với (BCD).
b) M, N là trung điểm của AC, AD nên MN là đường trung bình của tam giác ACD suy ra MN // CD.
Mà CD thuộc (BCD) nên MN // mp(BCD).

1:
a: \(D\in SA\subset\left(SAB\right);E\in SB\subset\left(SAB\right)\)
Do đó: \(DE\subset\left(SAB\right)\)
b: \(F\in AB\subset\left(SAB\right)\)
\(F\in DE\subset\left(CDE\right)\)
Do đó: \(F\in\left(SAB\right)\cap\left(CDE\right)\)
2:
\(N\in AB\subset\left(ABM\right);N\in CD\subset\left(SCD\right)\)
Do đó: \(N\in\left(ABM\right)\cap\left(SCD\right)\)
\(M\in SC\subset\left(SCD\right);M\in MB\subset\left(ABM\right)\)
Do đó: \(M\in\left(ABM\right)\cap\left(SCD\right)\)
Do đó: \(\left(ABM\right)\cap\left(SCD\right)=MN\)

Tham khảo:
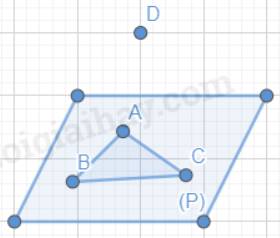
Tồn tại một và chỉ 1 mặt phẳng chứa hai đường thẳng AD và BD

Tham khảo:
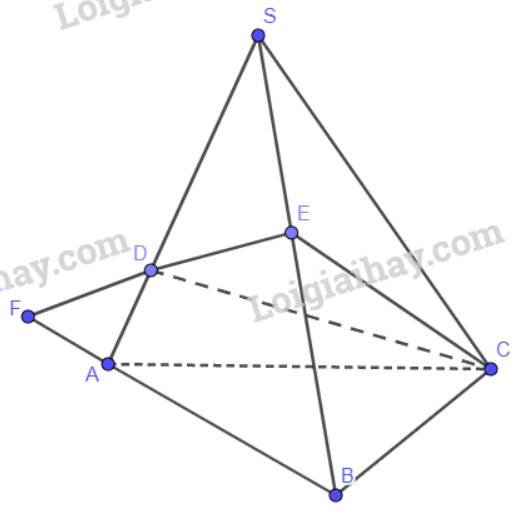
a) Ta có các điểm D, E đều nằm trong mp(SAB) nên đường thẳng DE nằm trong mp (SAB).
b) F thuộc AB suy ra F nằm trong mp (SAB).
F thuộc DE suy ra F nằm trong mp(CDE).
Do đó, F là điểm chung của hai mặt phẳng (SAB) và (CDE).

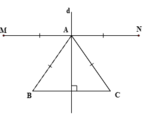
Ta có: B A M ^ = B ^ ( g t ) C A N ^ = C ^ ( g t )
Þ AM // BC; AN // BC (vì có cặp góc so le trong bằng nhau).
Þ 3 điểm M, A, N thẳng hàng (vì qua điểm A chỉ vẽ được một đường thẳng song song với BC).
Vậy MN // BC mà d ⊥ B C nên d ⊥ M N (1)
Ta có: A M = A B ; A N = A C
mà AB = AC (gt) nên AM = AN. (2)
Từ (1) và (2) Þ d là trung trực của MN

Mặt phẳng (ABC) chứa điểm A và đường thẳng d.
Do đó mp(ABC) cũng chứa hai đường thẳng AB và BC.
M ∈ BC mà BC ∈ (ABC) nên M ∈ (ABC)
Vì A ∈ (ABC) và M ∈ (ABC) nên mọi điểm thuộc AM đều thuộc (ABC) hay AM ⊂ (ABC)