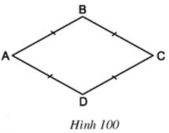
Chứng minh rằng tứ giác ABCD trên hình 100 cũng là một hình bình hành.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 10 2023
Sửa đề: Từ A,C hạ AH,CK lần lượt vuông góc với BD
Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔAHD=ΔCKB
=>AH=CK
AH\(\perp\)BD
CK\(\perp\)BD
Do đó: AH//CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
19 tháng 8 2021
a: Ta có: AE+EB=AB
DF+FC=DC
mà AE=FC
và AB=DC
nên EB=DF
Xét tứ giác EBFD có
EB//DF
EB=DF
Do đó: EBFD là hình bình hành
Suy ra: DE=BF
b: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
PT
1
CM
13 tháng 1 2018
- ABCD có các góc đối bằng nhau (đều là góc vuông) nên ABCD là hình bình hành
- ABCD là hình thang (vì AB // CD),
hai góc ở đáy: góc D = góc C ⇒ ABCD là hình thang cân
31 tháng 8 2021
a: Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(CN=ND=\dfrac{CD}{2}\)
mà AB=CD
nên AM=MB=CN=ND
Xét ΔMAP và ΔNCQ có
MA=CN
\(\widehat{A}=\widehat{C}\)
AP=CQ
Do đó: ΔMAP=ΔNCQ
b: Ta có: BQ+CQ=BC
AP+DP=AD
mà BC=AD
và CQ=AP
nên BQ=DP
Xét ΔMBQ và ΔNDP có
MB=ND
\(\widehat{B}=\widehat{D}\)
BQ=DP
Do đó: ΔMBQ=ΔNDP
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
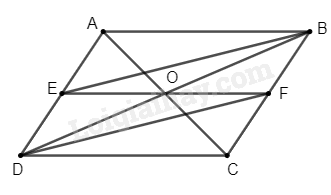
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AD = BC\); \(AD\) // \(BC\)
Mà \(E\), \(F\) là trung điểm của \(AD\), \(BC\) (gt)
Suy ra \(AE = ED = BF = FC\)
Xét tứ giác \(EBFD\) ta có:
\(ED = FB\) (cmt)
\(ED\) // \(BF\) (do \(AD\) // \(BC\))
Suy ra \(EDFB\) là hình bình hành
b) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\)
Mà \(DEBF\) là hình bình hành (gt)
Suy ra \(O\) cũng là trung điểm của \(EF\)
Suy ra \(E\), \(O\), \(F\) thẳng hàng
ABCD có các cặp cạnh đối bằng nhau ⇒ ABCD là hình bình hành