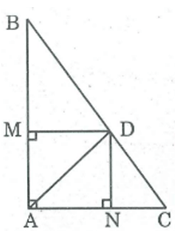
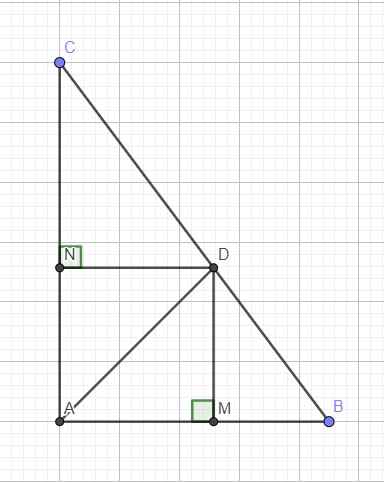
Cho tam giác ABC vuông tại A, đường phân giác AD. Gọi M, N là chân đường vuông góc kẻ từ D đến AB, AC. Chứng minh rằng tứ giác AMDN là hình vuông.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tứ giác AMDN có
\(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
Do đó: AMDN là hình chữ nhật
mà AD là tia phân giác
nên AMDN là hình vuông

bạn tự vẽ hình nk.
cm: vì m, n lần lượt là chân đg vuông góc kẻ từ d dến ab,ac
=> tứ giác AMDN là hình chữ nhật (có 3 góc vuông) (dh nb hcn)
mặt #: ad là đg phân giác của góc a
=> hcn AMDN là hình vuông vì có có đường chéo là đường phân giác của góc a(dh nb hv)

Xét tứ giác AMDN, ta có: ∠∠(MAN) = 900900 (gt)
DM ⊥ AB (gt)
⇒∠∠(AMD) = 900900
DN ⊥ AC (gt) ⇒∠∠(AND) = 900900
Suy ra tứ giác AMDN là hình chữ nhật
(vì có ba góc vuông), có đường chéo AD là đường phân giác của A
Vậy hình chữ nhật AMDN là hình vuông

a: Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{BD}{30}=\dfrac{CD}{40}\)
=>\(\dfrac{BD}{3}=\dfrac{CD}{4}\)
mà BD+CD=BC=50cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{50}{7}\)
=>\(BD=3\cdot\dfrac{50}{7}=\dfrac{150}{7}\left(cm\right);CD=4\cdot\dfrac{50}{7}=\dfrac{200}{7}\left(cm\right)\)
b: Xét tứ giác AMDN có
\(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
=>AMDN là hình chữ nhật
Hình chữ nhật AMDN có AD là phân giác của góc MAN
nên AMDN là hình vuông

\(\text{GIẢI :}\)
Chứng minh :
Ta có : M là chân đường vuông góc kẻ từ A đến AB \(\Rightarrow\text{ }\widehat{\text{M}}=90^{\text{o}}\).
N là chân đường vuông góc kẻ từ A đến AC \(\Rightarrow\text{ }\widehat{\text{N}}=90^{\text{o}}\)
Xét \(\diamond\text{AMDN}\) có \(\widehat{\text{A}}=\widehat{\text{M}}=\widehat{\text{N}}=90^{\text{o}}\)\(\Rightarrow\text{ }\diamond\text{AMDN}\) là hình chữ nhật.
mà AD là đường phân giác của góc A \(\Rightarrow\text{ }\diamond\text{AMDN}\) là hình vuông.

a.
\(AB^2+AC^2=4,5^2+6^2=56,25\)
\(BC^2=7,5^2=56,25\)
\(\Rightarrow AB^2+AC^2=BC^2\Rightarrow\Delta ABC\) vuông tại A theo Pitago đảo
b.
Theo định lý phân giác: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow DB=\dfrac{3}{4}DC\)
Mà \(DB+DC=BC=7,5\)
\(\Rightarrow\dfrac{3}{4}DC+DC=7,5\Rightarrow DC=\dfrac{30}{7}\left(cm\right)\)
Do DN và AB cùng vuông góc AC \(\Rightarrow DN||AB\)
Áp dụng định lý Talet:
\(\dfrac{DN}{AB}=\dfrac{DC}{BC}=\dfrac{4}{7}\Rightarrow DN=\dfrac{4}{7}AB=\dfrac{18}{7}\left(cm\right)\)
Tứ giác AMDN là hình chữ nhật (có 3 góc vuông)
Mà AD là đường chéo đồng thời là phân giác theo giả thiết
\(\Rightarrow AMDN\) là hình vuông
\(\Rightarrow S_{AMDN}=DN^2=\dfrac{324}{49}\approx6,6\left(cm^2\right)\)

Xét tứ giác AMDN, ta có: ∠ (MAN) = 90 0 (gt)
DM ⊥ AB (gt)
⇒ ∠ (AMD) = 90 0
DN ⊥ AC (gt) ⇒ ∠ (AND) = 90 0
Suy ra tứ giác AMDN là hình chữ nhật
(vì có ba góc vuông), có đường chéo AD là đường phân giác của A
Vậy hình chữ nhật AMDN là hình vuông
*Xét AMDN, có: (gt) =>AMDN là hình chữ nhật.
(gt) =>AMDN là hình chữ nhật.
Ta lại có: AD là đường phân giác (gt) =>AMDN là hình vuông(đpcm).
(gt) =>AMDN là hình vuông(đpcm).
CHÚC BẠN HỌC TỐT NHA!!