Giải các phương trình sau:
a)
b)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

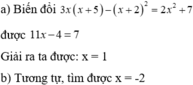

a) \(\sqrt {3{x^2} - 6x + 1} = \sqrt { - 2{x^2} - 9x + 1} \)
Bình phương hai vế của phương trình \(\sqrt {3{x^2} - 6x + 1} = \sqrt { - 2{x^2} - 9x + 1} \) ta được
\(3{x^2} - 6x + 1 = - 2{x^2} - 9x + 1\)
\( \Leftrightarrow 5{x^2} + 3x = 0\)
\( \Leftrightarrow x\left( {5x + 3} \right) = 0\)
\( \Leftrightarrow x = 0\) hoặc \(x = \frac{{ - 3}}{5}\)
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy cả hai giá trị x = 0 và \(x = \frac{{ - 3}}{5}\) đều thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là \(S = \left\{ {0;\frac{{ - 3}}{5}} \right\}\)
b) \(\sqrt {2{x^2} - 3x - 5} = \sqrt {{x^2} - 7} \)
Bình phương hai vế của phương trình \(\sqrt {2{x^2} - 3x - 5} = \sqrt {{x^2} - 7} \) , ta được
\(2{x^2} - 3x - 5 = {x^2} - 7\)
\( \Leftrightarrow {x^2} - 3x + 2 = 0\)
\( \Leftrightarrow x = 1\) hoặc \(\)\(x = 2\)
Thay lần lượt giá trị của x vào phương trình đã cho, ta thấy không có giá trị nào của x thỏa mãn.
Vậy phương trình đã cho vô nghiệm.

a) \(\dfrac{3}{x-7}+\dfrac{2}{x+7}=\dfrac{5}{x^2-49}\)
(ĐKXĐ: x khác 7; x khác -7)
<=>\(\dfrac{3.\left(x+7\right)}{\left(x-7\right).\left(x+7\right)}+\dfrac{2.\left(x-7\right)}{\left(x+7\right).\left(x-7\right)}=\dfrac{5}{\left(x+7\right).\left(x-7\right)}\)
=> 3x + 21 + 2x - 14 = 5
<=> 3x + 2x = 5 + 14 - 21
<=> 5x = -2
<=> x = \(\dfrac{-2}{5}\)
Vậy S = { \(\dfrac{-2}{5}\) }
b) \(\dfrac{2x-1}{3}-\dfrac{x+3}{2}>1+\dfrac{5x}{6}\)
<=> \(\dfrac{2.\left(2x-1\right)}{3.2}-\dfrac{3.\left(x+3\right)}{3.2}>\dfrac{1.6}{6}+\dfrac{5x}{6}\)
=> 4x - 2 - 3x - 9 > 6 + 5x
<=> 4x - 3x - 5x > 6 + 9 + 2
<=> -4x > 17
<=> \(\dfrac{-17}{4}\)
Vậy S = { \(\dfrac{-17}{4}\) }

a. 3(x-2)-10=5(2x + 1)
<=> 3x - 6 - 10 = 10x + 5
<=> 3x - 10x = 5 + 6 + 10
<=> -7x = 21
<=> x = -3
b. 3x + 2=8 -2(x-7)
<=> 3x + 2 = 8 - 2x + 14
<=> 3x + 2x = 8 + 14 - 2
<=> 5x = 20
<=> x = 4
c. 2x-(2+5x)= 4(x + 3)
<=> 2x - 2 - 5x = 4x + 12
<=> 2x - 5x - 4x = 12 + 2
<=> -7x = 14
<=> x = -2
d. 5-(x +8)=3x + 3(x-9)
<=> 5 - x - 8 = 3x + 3x - 27
<=> -x - 3x - 3x = -27 + 8 - 5
<=> -7x = -24
<=> x = 24/7
e. 3x - 18 + x= 12-(5x + 3)
<=> 3x - 18 + x = 12 - 5x - 3
<=> 3x + x - 5x = 12 - 3 + 18
<=> -x = 27
<=> x = - 27
a. 3(x-2)-10=5(2x + 1)
<=> 3x - 6 - 10 = 10x + 5
<=> 3x - 10x = 5 + 6 + 10
<=> -7x = 21
<=> x = -3
b. 3x + 2=8 -2(x-7)
<=> 3x + 2 = 8 - 2x + 14
<=> 3x + 2x = 8 + 14 - 2
<=> 5x = 20
<=> x = 4
c. 2x-(2+5x)= 4(x + 3)
<=> 2x - 2 - 5x = 4x + 12
<=> 2x - 5x - 4x = 12 + 2
<=> -7x = 14
<=> x = -2
d. 5-(x +8)=3x + 3(x-9)
<=> 5 - x - 8 = 3x + 3x - 27
<=> -x - 3x - 3x = -27 + 8 - 5
<=> -7x = -24
<=> x = 24/7
e. 3x - 18 + x= 12-(5x + 3)
<=> 3x - 18 + x = 12 - 5x - 3
<=> 3x + x - 5x = 12 - 3 + 18
<=> -x = 27
<=> x = - 27

a) \(\sqrt {11{x^2} - 14x - 12} = \sqrt {3{x^2} + 4x - 7} \)
\(\begin{array}{l} \Rightarrow 11{x^2} - 14x - 12 = 3{x^2} + 4x - 7\\ \Rightarrow 8{x^2} - 18x - 5 = 0\end{array}\)
\( \Rightarrow x = - \frac{1}{4}\) và \(x = \frac{5}{2}\)
Thay nghiệm vừa tìm được vào phương trình \(\sqrt {11{x^2} - 14x - 12} = \sqrt {3{x^2} + 4x - 7} \) ta thấy chỉ có nghiệm \(x = \frac{5}{2}\) thảo mãn phương trình
Vậy nhiệm của phương trình đã cho là \(x = \frac{5}{2}\)
b) \(\sqrt {{x^2} + x - 42} = \sqrt {2x - 30} \)
\(\begin{array}{l} \Rightarrow {x^2} + x - 42 = 2x - 3\\ \Rightarrow {x^2} - x - 12 = 0\end{array}\)
\( \Rightarrow x = - 3\) và \(x = 4\)
Thay vào phương trình \(\sqrt {{x^2} + x - 42} = \sqrt {2x - 30} \) ta thấy không có nghiệm nào thỏa mãn
Vậy phương trình đã cho vô nghiệm
c) \(2\sqrt {{x^2} - x - 1} = \sqrt {{x^2} + 2x + 5} \)
\(\begin{array}{l} \Rightarrow 4.\left( {{x^2} - x - 1} \right) = {x^2} + 2x + 5\\ \Rightarrow 3{x^2} - 6x - 9 = 0\end{array}\)
\( \Rightarrow x = - 1\) và \(x = 3\)
Thay hai nghiệm trên vào phương trình \(2\sqrt {{x^2} - x - 1} = \sqrt {{x^2} + 2x + 5} \) ta thấy cả hai nghiệm đếu thỏa mãn phương trình
Vậy nghiệm của phương trình \(2\sqrt {{x^2} - x - 1} = \sqrt {{x^2} + 2x + 5} \) là \(x = - 1\) và \(x = 3\)
d) \(3\sqrt {{x^2} + x - 1} - \sqrt {7{x^2} + 2x - 5} = 0\)
\(\begin{array}{l} \Rightarrow 3\sqrt {{x^2} + x - 1} = \sqrt {7{x^2} + 2x - 5} \\ \Rightarrow 9.\left( {{x^2} + x - 1} \right) = 7{x^2} + 2x - 5\\ \Rightarrow 2{x^2} + 7x - 4 = 0\end{array}\)
\( \Rightarrow x = - 4\) và \(x = \frac{1}{2}\)
Thay hai nghiệm trên vào phương trình \(3\sqrt {{x^2} + x - 1} - \sqrt {7{x^2} + 2x - 5} = 0\) ta thấy chỉ có nghiệm \(x = - 4\) thỏa mãn phương trình
Vậy nghiệm của phương trình trên là \(x = - 4\)

a) Ta có: \(\left|x^2-x+2\right|-3x-7=0\)
\(\Leftrightarrow\left|x^2-x+2\right|=3x+7\)
\(\Leftrightarrow x^2-x+2=3x+7\)(Vì \(x^2-x+2>0\forall x\))
\(\Leftrightarrow x^2-x+2-3x-7=0\)
\(\Leftrightarrow x^2-4x-5=0\)
\(\Leftrightarrow x^2-5x+x-5=0\)
\(\Leftrightarrow x\left(x-5\right)+\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
Vậy: S={5;-1}
bạn giải giúp mình câu b nữa với
mai mình phải nộp bài rồi!!!![]()

a) ĐKXĐ: \(x\notin\left\{5;-5\right\}\)
Ta có: \(\dfrac{-\left(x^2+5\right)}{x^2-25}=\dfrac{3}{x+5}+\dfrac{x}{x-5}\)
\(\Leftrightarrow\dfrac{3\left(x-5\right)}{\left(x+5\right)\left(x-5\right)}+\dfrac{x\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}=\dfrac{-x^2-5}{\left(x-5\right)\left(x+5\right)}\)
Suy ra: \(3x-15+x^2+5x+x^2+5=0\)
\(\Leftrightarrow2x^2+8x-10=0\)
\(\Leftrightarrow2x^2+10x-2x-10=0\)
\(\Leftrightarrow2x\left(x+5\right)-2\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(2x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=0\\2x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\2x=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\left(loại\right)\\x=1\left(nhận\right)\end{matrix}\right.\)
Vậy: S={1}
`a,(-(x^2+5))/(x^2-25)=3/(x+5)+x/(x-5)`
`ĐK:x ne +-5`
`pt<=>-x^2+5=3(x-5)+x(x+5)`
`<=>-x^2+5=3x-15+x^2+5x`
`<=>-x^2+5=x^2+8x-15`
`<=>2x^2+8x-20=0`
`<=>x^2+4x-5=0`
`<=>x^2-x+5x-5=0`
`<=>x(x-1)+5(x-1)=0`
`<=>` $\left[ \begin{array}{l}x=1\\x=-5\end{array} \right.$
Vậy `S={1,-5}`

\(a,=>x^3-2x^2+4x+2x^2-4x+8-x^3+2x-15=0\)
\(< =>2x-7=0< =>x=\dfrac{7}{2}\)
b,\(=>x\left(x^2-25\right)-\left(x+2\right)\left(x^2-2x+4\right)-3=0\)
\(< =>x^3-25x-x^3+2x^2-4x-2x^2+4x-8-3=0\)
\(< =>-25x-11=0\)
\(< =>x=-0,44\)

a.\(x^2-25=8\left(5-x\right)\)
\(\Leftrightarrow\left(x-5\right)\left(x+5\right)-8\left(5-x\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+5\right)+8\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+13\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-13\end{matrix}\right.\)
b.\(\dfrac{x-2}{x+2}-\dfrac{2\left(x-11\right)}{x^2-4}=\dfrac{3}{x-2}\) ; \(ĐK:x\ne\pm2\)
\(\Leftrightarrow\dfrac{\left(x-2\right)\left(x-2\right)-2\left(x-11\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\left(x-2\right)^2-2\left(x-11\right)=3\left(x+2\right)\)
\(\Leftrightarrow x^2-4x+4-2x+22=3x+6\)
\(\Leftrightarrow x^2-9x+20=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\left(tm\right)\\x=4\left(tm\right)\end{matrix}\right.\)

(a) Điều kiện: \(\left\{{}\begin{matrix}x+1\ge0\\x-5>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x>5\end{matrix}\right.\Rightarrow x>5\).
Phương trình tương đương: \(\sqrt{x+1}=2\sqrt{x-5}\)
\(\Leftrightarrow x+1=4\left(x-5\right)\Leftrightarrow x=7\left(TM\right)\).
Vậy: \(S=\left\{7\right\}.\)
(b) Phương trình tương đương: \(x^2-1=8\)
\(\Leftrightarrow x^2=9\Leftrightarrow x=\pm3\).
Vậy: \(S=\left\{\pm3\right\}\)
a: ĐKXĐ: x+1>=0 và x-5>0
=>x>5
\(\dfrac{\sqrt{x+1}}{\sqrt{x-5}}=2\)
=>\(\sqrt{\dfrac{x+1}{x-5}}=2\)
=>\(\dfrac{x+1}{x-5}=4\)
=>4x-20=x+1
=>3x=21
=>x=7
b: ĐKXĐ: \(x\in R\)
\(\sqrt[3]{x^2-1}=2\)
=>x^2-1=8
=>x^2=9
=>x=3 hoặc x=-3

\(a,\Leftrightarrow x^2+2x+1+2x+3-2\sqrt{2x+3}+1=0\\ \Leftrightarrow\left(x+1\right)^2+\left(\sqrt{2x+3}-1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=-1\\2x+3=1\end{matrix}\right.\Leftrightarrow x=-1\left(N\right)\)
\(b,\Leftrightarrow3x^2+3x-2\sqrt{x^2+x}=0\left(x\le-1;x\ge0\right)\\ \Leftrightarrow3x\left(x-1\right)-2\sqrt{x\left(x+1\right)}=0\\ \Leftrightarrow\sqrt{x\left(x+1\right)}\left(3\sqrt{x\left(x-1\right)}-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x\left(x-1\right)=0\\\sqrt{x\left(x-1\right)}=\dfrac{2}{3}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x^2-x-\dfrac{4}{9}=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\9x^2-9x-4=0\left(1\right)\end{matrix}\right.\)
\(\Delta\left(1\right)=81-4\left(-4\right)\cdot9=225\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=\dfrac{9-15}{18}\\x=\dfrac{9+15}{18}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(N\right)\\x=1\left(N\right)\\x=-\dfrac{1}{3}\left(L\right)\\x=\dfrac{4}{3}\left(N\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=\dfrac{4}{3}\end{matrix}\right.\)