Theo công suất có loại điện trở:
A. Điện trở công suất nhỏ
B. Điện trở công suất lớn
C. Điện trở công suất vừa
D. Cả 3 đáp án trên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 11 2021
b)Công suất tiêu thụ trên mạch 2:
\(P_2=\left(\dfrac{\xi}{r+R_1+R_2}\right)^2\cdot R_2=\left(\dfrac{24}{4+6+R_2}\right)^2\cdot R_2=\left(\dfrac{24}{10+R_2}\right)^2\cdot R_2\) Áp dụng bđt Cô-sy:
\(P_2=\dfrac{24^2}{(\dfrac{10}{\sqrt{R_2}}+\sqrt{R_2})^2}\le\dfrac{24^2}{10\cdot4}=14,4W\)
Dấu "=" xảy ra\(\Leftrightarrow10=R_2\)
19 tháng 11 2021
a)Công suất tiêu thụ mạch ngoài:
\(P_N=\left(\dfrac{\xi}{r+R_N}\right)^2\cdot R_N=\dfrac{\xi^2}{\left(\dfrac{r}{\sqrt{R_N}}+\sqrt{R_N}\right)^2}\le\dfrac{\xi^2}{4r}=\dfrac{24^2}{4\cdot4}=36\)
(Bất đẳng thức Cô-sy)
Dấu "=" xảy ra\(\Leftrightarrow r=R_N=4\Omega\)
\(\Rightarrow\dfrac{1}{4}=\dfrac{1}{6}+\dfrac{1}{R_2}\Rightarrow R_2=12\Omega\)
VT
5 tháng 6 2017
Công suất tiêu thụ trên điện trở Rx:
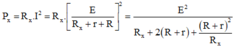
Áp dụng đẳng thức Cô-si cho hai số dương Rx và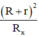 
Ta có:
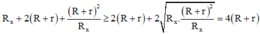
Dấu "=" xảy ra khi Rx = R + r = 1,2Ω
Giá trị cực đại của cống suất mạch ngoài:
VT
6 tháng 5 2018
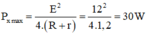
Hướng dẫn giải
Giả sử các nguồn được ghép thành m dãy song song, mỗi dãy có n nguồn ghép nối tiếp.
Ta có suất điện động và điện trở trong của bộ nguồn là: E b = n E ; r b = 3 n m
a) Cách mắc nguồn để công suất tiêu thụ của R là lớn nhất:
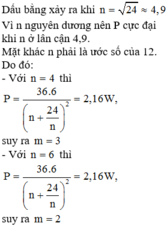
Như vậy để công suất tiêu thụ của R là lớn nhất thì phải mắc nguồn thành 3 dãy song song, mỗi dãy gồm 4 nguồn ghép nối tiếp hoặc mắc nguồn thành 2 dãy song song, mỗi dãy gồm 6 nguồn ghép nối tiếp.
b) Cách măc nguồn để công suất tiêu hao của mỗi nguồn là nhỏ nhất:
Công suất tiêu hao trên mỗi nguồn là:
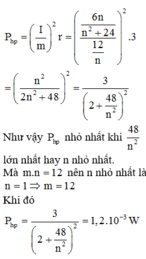
Như vậy để công suất tiêu hao trên mỗi nguồn là nhỏ nhất thì phải mắc nguồn thành 12 dãy song song, mỗi dãy gồm 1 nguồn
VT
10 tháng 2 2019
a) Tìm công suất tỏa nhiệt trên điện trở R 4
Chọn chiều dòng điện qua các điện trở trong mạch như hình vẽ.
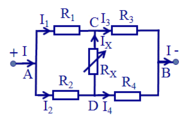
* Xét tại nút A ta có: I = I 1 + I 2 (1)
Với vòng kín ACDA ta có:
I 1 R 1 - I X R X - I 2 R 2 = 0 (2)
Thế (1) vào (2) ta được biểu thức I :
I 1 R 1 - I X R X - ( I - I 1 ) R 2 = 0 I 1 R 1 - I X R X - I R 2 + I 1 R 2 = 0 I 1 ( R 1 + R 2 ) = I X R X + I R 2 ⇒ I 1 = I X . R X + I . R 2 R 1 + R 2 = I X . R X + I . R 4 R (3)
* Xét tại nút B ta có: I 3 = I - I 4 (4)
Với vòng kín BCDB ta có:
I 3 R 3 - I X R X + I 4 R 4 = 0 I 3 R - I X R X + I 4 X = 0 (5)
Thế (4) vào (5) ta có biểu thức
I
4
:
(
I
-
I
4
)
R
-
I
X
R
X
+
I
4
R
=
0
I
.
R
+
I
4
R
-
I
X
R
X
+
I
4
R
=
0
⇒ I 4 = I . R + I X R X 2 R (6)
Từ (3) và (6) ta có: = 2 ð = =
Vậy công suất tỏa nhiệt trên R 4 khi đó là P 4 = 4 3 P 1 = 12 W .
b) Tìm R X theo R để công suất tỏa nhiệt trên R X cực đại
Từ (4) và (5) ta có biểu thức I 3 :
I 3 R - I X R X + ( I - I 3 ) R = 0 I 3 R - I X R X + I R - I 3 R = 0 ⇒ I 3 = I . R - I X R X 2 R (7)
Ta có: U = U A B = U A C + U C B = I 1 . R 1 + I 3 R 3 U = I 1 3 R + I 3 R (8)
Thế (3) và (7) vào (8) ta được:
U = I X R X + I . R 4 R . 3 R + I . R - I X R X 2 R . R 4 U = 3 . I X R X + 3 . I . R + 2 I . R - 2 I X R X 4 U = 5 . I . R + I X R X (9)
Tính I:
Ta có:
I = I 1 + I 2 = I 1 + I 4 + I X = 3 I 1 + I X = 3 . I X R X + I R 4 R + I X ⇒ 4 . I . R = 3 I X R X + 3 . I . R + 4 . I X . R ⇒ I R = 3 I X . R X + 4 . I X . R t h a y v à o ( 9 ) t a đ ư ợ c : 4 U = 5 . ( 3 I X . R X + 4 I X . R ) + I X R X = 15 . I X . R X + 20 I X R + I X R X = 16 . I X R X + 20 I X R ⇒ I X = U 4 R X + 5 R
Hai số dương 4 R x và 5 R R x có tích 4 R x . 5 R R x = 20 R không đổi thì theo bất đẳng thức Côsi, tổng của hai số đó nhỏ nhất khi hai số đó bằng nhau nghĩa là khi 4 R x = 5 R R x ⇒ R x = 1 , 25 R ; mẫu số ở vế phải của biểu thức (10) nhỏ nhất nghĩa là P X cực đại. Vậy PX cực đại khi R X = 1 , 25 R .
VT
14 tháng 7 2018
Đáp án D
Gọi R t là điện trở tổng cộng ở mạch ngoài thì R t = R 1 R x R 1 + R x = 2 R x 2 + R x
U N = R t I = 2R x 2 + R x E 2R x 2 + R x + r = 8 R x 1 + R x P R x = R x I 2 = U N 2 R x = 8 R x 1 + R x 2 R x = 64 R x + 1 R x 2
Theo bất đẳng thức Cô si R x + 1 R x ≥ 2 nên P R x ≤ 64 2 2 = 16
Dấu “=” xảy ra khi R x = 1 ⇒ P R x ( max ) = 16 W
Đáp án D
Cả 3 đáp án trên