Tìm các giá trị lượng giác của các góc 120o, 150o.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


thì ai cần bố học lớp 5 giải đâu, toán hình nâng cao lớp 7 mà :v

\(\sin \left( {45^\circ } \right) = \frac{{\sqrt 2 }}{2};\,\,\cos \left( {45^\circ } \right) = \frac{{\sqrt 2 }}{2};\,\,\tan \left( {45^\circ } \right) = \frac{1}{2};\,\,\cot \left( {45^\circ } \right) = 2\)

Tham khảo:
Lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^o}\), H là hình chiếu vuông góc của M trên Oy.
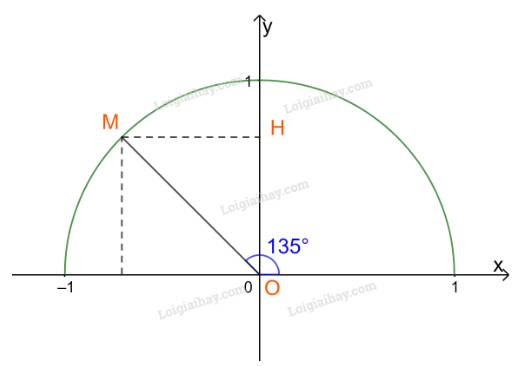
Ta có: \(\widehat {MOy} = {135^o} - {90^o} = {45^o}\).
Tam giác OMH vuông cân tại H nên \(OH = MH = \frac{{OM}}{{\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}.\)
Vậy tọa độ điểm M là \(\left( { - \frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right).\)
Vậy theo định nghĩa ta có:
\(\begin{array}{l}\;\sin {135^o} = \frac{{\sqrt 2 }}{2};\;\;\cos {135^o} = - \frac{{\sqrt 2 }}{2};\\\;\tan {135^o} = - 1;\;\;\cot {135^o} = - 1.\end{array}\)
Chú ý
Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc \({135^o}\)
Với các loại máy tính fx-570 ES (VN hoặc VN PLUS) ta làm như sau:
Bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ)
Tính \(\sin {135^o}\), bấm phím: sin 1 3 5 \(^o\)’’’ = ta được kết quả là \(\frac{{\sqrt 2 }}{2}\)
Tính \(\cos {135^o}\),bấm phím: cos 1 3 5 \(^o\)’’’ = ta được kết quả là \(\frac{{ - \sqrt 2 }}{2}\)
Tính \(\tan {135^o}\), bấm phím: tan 1 3 5 \(^o\)’’’ = ta được kết quả là \( - 1\)
(Để tính \(\cot {135^o}\), ta tính \(1:\tan {135^o}\))

Ta có: y ' = 4 x 3 + 4 m x ; y ' = 0 ⇔ 4 x x 2 + m = 0
Đồ thị của hàm số có ba điểm cực trị ⇔ phương trình 4 x x 2 + m có ba nghiệm phân biệt ⇔ m < 0 . Khi đó phương trình y' = 0 có ba nghiệm là
x = 0 x = - - m x = - m
Gọi A 0 ; m 2 + m , B - - m ; m , C - m ; m là các điểm cực trị
Ta có A B = - - m ; m 2 , A C = - m ; m 2
Vì A ∈ O x , B và C là hai điểm đối xứng nhau qua Oy nên ∆ A B C cân tại A. Như vậy góc 120 o chính là A ^
Ta có
cos A = - 1 2 ⇔ A B → . A C → A B → . A C → = - 1 2 ⇔ m + m 4 m 4 - m = - 1 2 ⇔ 3 m 4 + m = 0 ⇔ 3 m 3 + 1 = 0 ⇔ m = - 1 3 3
Đáp án D

Tham khảo:
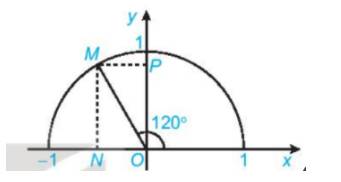
Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {120^o}\)
Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.

Vì \(\widehat {xOM} = {120^o} > {90^o}\) nên M nằm bên trái trục tung.
Khi đó:\(\;\cos {120^o} = - \,\;\overline {ON} ,\;\;\sin {120^o} = \overline {OP} \)
Vì \(\widehat {xOM} = {120^o}\) nên \(\widehat {NOM} = {180^o} - {120^o} = {60^o}\) và \(\widehat {POM} = {120^o} - {90^o} = {30^o}\)
Vậy các tam giác \(\Delta MON\) và \(\Delta MOP\) vuông tại N, p và có một góc bằng \({30^o}\)
\( \Rightarrow ON = MP = \frac{1}{2}OM = \frac{1}{2}\)(Trong tam giác vuông, cạnh đối diện góc \({30^o}\) bằng một nửa cạnh huyền)
Và \(OP = MN = \sqrt {O{M^2} - O{N^2}} = \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}\)
Vậy điểm M có tọa độ là \(\left( { - \frac{1}{2};\frac{{\sqrt 3 }}{2}} \right)\).
Và \(\cos {120^o} = - \frac{1}{2};\;\;\;\sin {120^o} = \frac{{\sqrt 3 }}{2}\)
\(\begin{array}{l}\; \Rightarrow \;\tan {120^o} = \frac{{\sin {{120}^o}}}{{\cos {{120}^o}}} = \frac{{\sqrt 3 }}{2}:\left( { - \frac{1}{2}} \right) = - \sqrt 3 ;\\\cot {120^o} = \frac{{\cos {{120}^o}}}{{\sin {{120}^o}}} = \left( { - \frac{1}{2}} \right):\frac{{\sqrt 3 }}{2} = \frac{{ - 1}}{{\sqrt 3 }} = - \frac{{\sqrt 3 }}{3}.\end{array}\)
Chú ý
Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc \({120^o}\)
Với các loại máy tính fx-570 ES (VN hoặc VN PLUS) ta làm như sau:
Bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ)
Tính \(\sin {120^o}\), bấm phím: sin 1 2 0 \(^o\)’’’ = ta được kết quả là \(\frac{{\sqrt 3 }}{2}\)
Tính \(\cos {120^o}\),bấm phím: cos 1 2 0 \(^o\)’’’ = ta được kết quả là \(\frac{{ - 1}}{2}\)
Tính \(\tan {120^o}\), bấm phím: tan 1 2 0 \(^o\)’’’ = ta được kết quả là \( - \sqrt 3 \)
( Để tính \(\cot {120^o}\), ta tính \(1:\tan {120^o}\))

Các số sinα; cosα; tanα; cotα được gọi là giá trị lượng giác của góc α, với 0o ≤ α ≤ 180o.

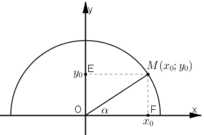
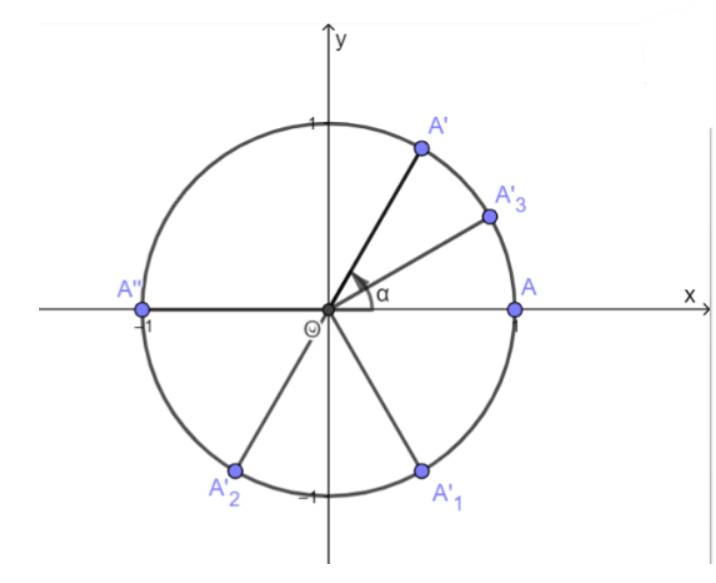
a) Trên nửa đường tròn lượng giác nằm phía trên trục hoành, xác định điểm M(x0; y0) sao cho 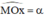
Khi đó ta có:
sin α = y0
cos α = x0
tan α = y0 / x0
cot α = x0 / y0
b) Gọi E, F là hình chiếu của M trên Oy, Ox.
Khi α < 90º thì x0 > 0, y0 > 0
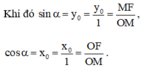
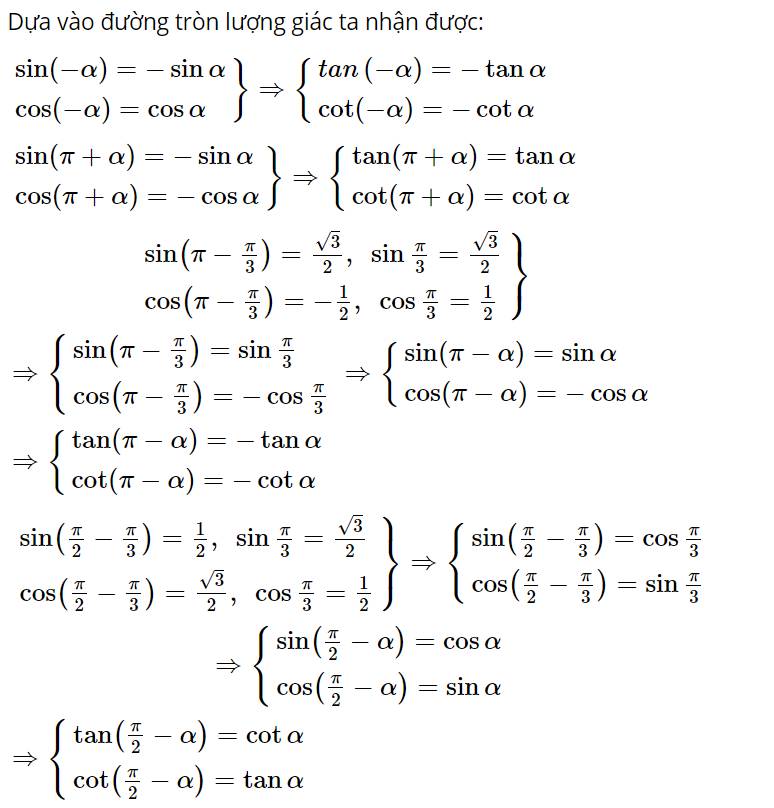
Các giá trị lượng giác của góc 120o là:
sin 120º = sin (180º – 60º) = sin 60º = √3/2.
cos 120º = cos(180º – 60º) = –cos 60º = –1/2
tan 120º = sin 120º / cos 120º = –√3
cot 120º = cos 120º / sin 120º = –1/√3
Các giá trị lượng giác của góc 150º là:
sin 150º = sin ( 180º – 30º ) = sin 30º = 1/2
cos 150º = –cos ( 180º – 30º ) = –cos 30º = (–√3)/2
tan 150º = sin 150º / cos 150º = –1/√3
cot 150º = cos 150º / sin 150º = –√3.