Cho AOB là tam giác cân tại O có OA = a và có các đường cao OH và AK. Giả sử ∠AOH = α. Tính AK và OK theo a và α.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có = 2α => Trong tam giác OKA có:
AK = OA.sin. => AK = a.sin2α
OK =OA.cos. => OK = a.cos2α


Hướng dẫn giải:
Ta có \(\widehat{AOB}\) = 2α => Trong tam giác OKA có:
AK = OA.sin.\(\widehat{AOK}\) => AK = a.sin2α
OK =OA.cos.\(\widehat{AOK}\) => OK = a.cos2α

\(\widehat{O}=2\widehat{AOH}=2\alpha\)
Trong tam giác vuông AOK:
\(AK=OA.sin\widehat{O}=a.sin\left(2\alpha\right)\)
Trong tam giác vuông AOH:
\(OH=OA.cos\widehat{AOH}=a.cos\alpha\)

Đáp án D
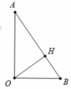
Ta có O A . sin O A H ^ = O H = a ⇒ O A = 2 a
Lại có O B = O A tan A ^ = 2 a 3 suy ra thể tích khối nón tròn xoay tạo bởi tam giác AOB khi quay quanh trục OA là V = 1 3 πOB 2 . OA = 8 9 πa 3
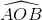 = 2α => Trong tam giác OKA có:
= 2α => Trong tam giác OKA có: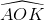 => AK = a.sin2α
=> AK = a.sin2α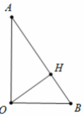
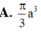
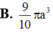
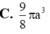
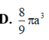

ΔAOB cân tại O nên OH là đường cao đồng thời là đường phân giác
Xét ΔOAK vuông tại K có: