Chứng minh hàm số y = |x| không có đạo hàm tại x = 0. Hàm số có đạt cực trị tại điểm đó không ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 1 2017
Hàm số có tập xác định D = R và liên tục trên R.
+ Chứng minh hàm số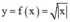 
không có đạo hàm tại x = 0.
Xét giới hạn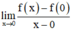 
:
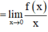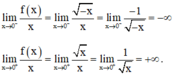
⇒ Không tồn tại giới hạn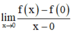 
Hay hàm số không có đạo hàm tại x = 0.
+ Chứng minh hàm số đạt cực tiểu tại x = 0 (Dựa theo định nghĩa).
Ta có : f(x) > 0 = f(0) với ∀ x ∈ (-1 ; 1) và x ≠ 0
⇒ Hàm số y = f(x) đạt cực tiểu tại x = 0.
PT
1
CM
9 tháng 11 2018
Hàm số:
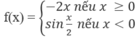
Không có đạo hàm tại x = 0 vì:
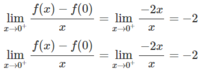
Mặt khác, với x < 0 thì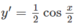 
với x > 0 thì y’ = -2 < 0
Bảng biến thiên:
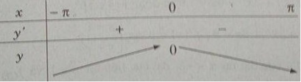
Từ đó ta thấy hàm số đạt cực đại tại x = 0 và y C Đ = y(0) = 0.
CM
8 tháng 4 2019
Hàm số:
f
x
=
-
2
x
nếu
x
≥
0
sin
x
2
nếu
x
<
0
Không có đạo hàm tại x = 0 vì:
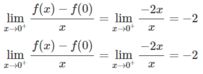
Mặt khác, với x < 0 thì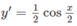 
với x > 0 thì y’ = -2 < 0
Bảng biến thiên:
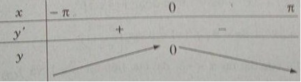
Từ đó ta thấy hàm số đạt cực đại tại x = 0 và y CD = y(0) = 0.
CM
13 tháng 2 2019
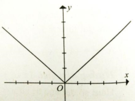
Đồ thị hàm số y = |x| có dạng hình vẽ.
Từ đồ thị trong hình ta có hàm số y = |x| liên tục tại x = 0 nhưng không có đạo hàm tại điểm đó. Sử dụng định nghĩa cực trị ta có hàm số y = |x| đạt cực tiểu tại x = 0
Do đó mệnh đề 1 và 4 đúng. Chọn đáp án C
CM
30 tháng 11 2017
Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng
CM
24 tháng 6 2018
Đáp án A
Mệnh đề 1) sai vì f ' x 0 = 0 chỉ là điều kiện cần chưa là điều kiện đủ để hàm số đạt cực trị tại x 0
Mệnh đề 2) Sai vì khi f ' x 0 = f ' ' x 0 = 0 có thể hàm số có thể đạt cực trị hoặc không đạt cực trị tại x 0 .
Mệnh đề 3) sai vì f ' x đổi dấu qua điểm x 0 thì điểm x 0 có thể là điểm cực đại hoặc điểm cực tiểu của hàm số.
Mệnh đề 4) Sai vì trong trường hợp này x 0 là điểm cực tiểu của đồ thị hàm số.
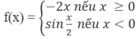
Vậy không tồn tại đạo hàm của hàm số tại x = 0.
Nhưng dựa vào đồ thị của hàm số y = |x|. Ta có hàm số đạt cực trị tại x = 0.