Trong các hình hộp chữ nhật có độ dài đường chéo bằng d, hãy tìm hình hộp chữ nhật có diện tích toàn phần lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
Giả độ dài các cạnh của khối hộp lần lượt là a; b; c khi đó T = 2ab + 2bc + 2ca = 36.
⇔ a b + b c + c a = 18 . Mặt khác A C ' = A B 2 + A D 2 + A A ' 2 = a 2 + b 2 + c 2 = 6
Khi đó a 2 + b 2 + c 2 = 36 a b + b c + c a = 18 ⇒ a + b + c 2 = 72 a b + b c + c a = 18 ⇔ a + b + c = 6 2 b a + c + a c = 18
Ta có: V = a b c = b . 18 - b a + c = b 18 - b 6 2 - b = b 3 - 6 2 b 2 + 18 b = f b
Xét f b = b 3 - 6 2 b 2 + 18 b , 0 < b < 6 2 ta có : f ' b = 3 b 2 - 12 2 b + 18 = 0 ⇔ b 2 - 4 b 2 + 6 = 0
⇔ [ b = 3 2 b = 3 ⇒ f 3 2 = 0 ; f 2 = 8 2 ⇒ M a x ( 0 ; 6 2 ) f b = 8 2 .

Giả sử hình hộp chữ nhật ấy có tên là ABCD.A'B'C'D' và các số liệu thống kê như hình vẽ
Bài làm:
Vì tam giác CDD' vuông tại D nên theo định lý Pytago:
\(CD'=\sqrt{CD^2+DD'^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
Vì A'D' vuông góc với D'C'
=> \(A'D'\perp mp\left(CDD'C'\right)\Rightarrow A'D'\perp D'C\)
=> Tam giác A'D'C vuông tại D' nên áp dụng định lý Pytago:
\(A'D'=\sqrt{A'C^2-CD'^2}=\sqrt{13^2-5^2}=12\left(cm\right)\)
=> Diện tích toàn phần của hình hộp chữ nhật đó là:
\(S_{tp}=S_{xp}+2S_đ=2.\left(3+4\right).12+2.3.4=192\left(cm^2\right)\)
Học tốt!!!!

1. Hình hộp chữ nhật đó có : - Chiều rộng là :1,3 x 2/3 = 13/15(dm)
- Diện tích xung quanh là : 2 x (1,3 +13/15) x 1 = 13/3(dm2)
- Diện tích toàn phần là : 13/3 + 1,3 x 13/15 x 2 = 494/75(dm2)
2. Diện tích xung quanh của thùng tôn là : 2 x (10+ 5) x 7 = 210(dm2)
Diện tích tôn để làm thùng là : 210 + 10 x 5 = 260(dm2)
3. Hộp giấy đó có : - Diện tích xung quanh là : 6 x 4 x 8 = 192(dm2)
- Diện tích toàn phần là : 192 + 6 x 6 x 2 = 264(dm2)
4. Hình hộp chữ nhật đó có : - Chiều rộng là : 12 x 1/3 = 4(cm) ; Chiều cao là : 4 : 2/3 = 6(cm)
- Diện tích xung quanh là : 2 x (12+ 4) x 6 = 192(cm2)
- Diện tích toàn phần là : 192 + 12 x 4 x 2 = 288(cm2)
5. Chiều cao của hình thang đó là : 3/4 x 2 : 5/8 = 2,4(m)
Bài 5 bạn phải thay "độ dài đáy" thành "tổng độ dài 2 đáy" thì đề mới chính xác.

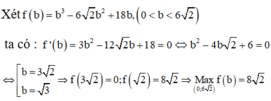
Gọi các kích thước của hình hộp lần lượt là a, b, c (a, b, c > 0)
Theo đề bài ta có a2 + b2 + c2= d2
Diện tích toàn phần của hình hộp là:
Dấu "=" xảy ra Û a = b = c.
Vậy hình hộp có diện tích toàn phần lớn nhất là hình lập phương.