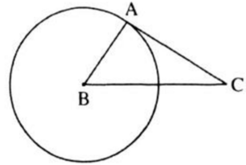
Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Vẽ đường tròn (B; BA). Chứng minh rằng AC là tiếp tuyến của đường tròn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: A B 2 + A C 2 = 3 2 + 4 2 = 25 B C 2 = 5 2 = 25
Nên A B 2 + A C 2 = B C 2
=> tam giác ABC vuông tại A hay AC ⊥ BA.
Đường thẳng AC đi qua điểm A của đường tròn và vuông góc với bán kính BA đi qua điểm A nên AC là tiếp tuyến của đường tròn.

Tam giác ABC vuông tại A (theo định lý Py-ta-go đảo)
⇒AC⊥AB,⇒AC⊥AB, do đó AC là tiếp tuyến.
Ta có: AB2 + AC2 = 32 + 42 = 25.
BC2 = 52 = 25.
Nên AB2 + AC2 = BC2.
Suy ra tam giác ABC vuông tại A hay AC ⊥ BA.
Đường thẳng AC đi qua điểm A của đường tròn và vuông góc với bán kính BA đi qua điểm A nên AC là tiếp tuyến của đường tròn.

Tam giác ABCABC có:
AB^2+AC^2=3^{2}+4^{2}=5^{2}AB2+AC2=32+42=52
Mặt khác: BC^{2}=5^{2}BC2=52
Vậy \mathrm{AB}^{2}+\mathrm{AC}^{2}=\mathrm{BC}^{2}AB2+AC2=BC2.
Do đó \widehat{BAC}=90^{\circ}BAC=90∘ (định lí Py-ta-go đảo).
CACA vuông góc với bán kính BABA tại AA nên CACA là tiếp tuyến của đường tròn (B)(B).

Ta có: A B 2 + A C 2 = 3 2 + 4 2 = 5 2 ⇒ A B 2 + A C 2 = B C 2
⇒ ∆ABC vuông tại A.
Diện tích tam giác ABC là:
S ∆ A B C = 1 2 A B . A C = 1 2 . 3 . 4 = 6 .
Nửa chu vi của tam giác là p = 1 / 2 ( 3 + 4 + 5 ) = 6 .
Bán kính đường tròn nội tiếp của tam giác ABC là:
r = S p = 6 6 = 1 . Chọn D.

a. \(BC^2=AB^2+AC^2\) nên ABC vuông tại A
b. Hệ thức lượng: \(AH=\dfrac{AB\cdot AC}{BC}=2,4\left(cm\right)\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\\ \Rightarrow\widehat{B}\approx53^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx37^0\)

Ta có: A B 2 + A C 2 = B C 2 ( 3 2 + 4 2 = 5 2 )
Suy ra, tam giác vuông tại A.
Diện tích tam giác ABC là: S = 1 2 . A B . A C = 6
Nửa chu vi tam giác: p = 3 + 4 + 5 2 = 6
Bán kính đường tròn nội tiếp của tam giác là: r = S p = 1
ĐÁP ÁN A
Ta có: AB2 + AC2 = 32 + 42 = 25
BC2 = 52 = 25
Nên AB2 + AC2 = BC2
=> tam giác ABC vuông tại A hay AC ⊥ BA.
Đường thẳng AC đi qua điểm A của đường tròn và vuông góc với bán kính BA đi qua điểm A nên AC là tiếp tuyến của đường tròn.