Đặt vật AB = 2 (cm) thẳng góc trục chính thấu kính phân kỳ có tiêu cự f = - 12 (cm), cách thấu kính một khoảng d = 12 (cm) thì ta thu được :
A. ảnh thật A’B’, cao 2cm
B. ảnh ảo A’B’, cao 2cm
C. ảnh ảo A’B’, cao 1 cm
D. ảnh thật A’B’, cao 1 cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\Delta A'B'O'\sim\Delta ABO\Rightarrow\dfrac{A'B'}{AB}=\dfrac{O'A'}{OA}\left(1\right)\)
\(\Delta FA'B'\sim\Delta FOI\Rightarrow\dfrac{FA'}{OF}=\dfrac{A'B'}{OI}\left(2\right)\)
Và OI=AB, Từ (1) và (2) \(\Rightarrow\dfrac{OA'}{OA}=\dfrac{FA'}{OF}\left(3\right)\)
Mà FA'=OF-OA'
Hay \(\dfrac{OA'}{OA}=\dfrac{OF-OA'}{OF}\) thay số: \(\dfrac{OA'}{36}=\dfrac{18-OA'}{18}\Rightarrow OA'=12\left(cm\right)\)
Và: \(\dfrac{A'B'}{AB}=\dfrac{OA'}{OA}\Rightarrow A'B'=\dfrac{AB.OA'}{OA}=\dfrac{4.12}{36}=1,33\left(cm\right)\)

a)Thấu kính hội tụ cho ảnh A'B' là ảnh thật.
Ảnh A'B' ngược chiều vật và nhỏ hơn vật.
b)Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{30}=\dfrac{1}{45}+\dfrac{1}{d'}\)
\(\Rightarrow d'=90cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{15}{h'}=\dfrac{45}{90}\)
\(\Rightarrow h'=A'B'=30cm\)

b)Ảnh thật.
c)Để ảnh thật cao gấp đôi vật \(\Rightarrow h'=2h\) thì:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{h}{2h}=\dfrac{d}{d'}=\dfrac{1}{2}\Rightarrow d'=2d\)
Khi đó vị trí cách thấu kính là:
\(d'=2d=2\cdot50=100cm\)

Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{5}{h'}=\dfrac{40}{15}\Rightarrow h'=1,875cm\)
Tiêu cự thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{40}+\dfrac{1}{15}=\dfrac{11}{120}\)
\(\Rightarrow f=\dfrac{120}{11}cm\approx10,91cm\)

Chọn câu B.
Vật AB cách thấu kính d = 30cm, vật ngoài khoảng OF nên cho ảnh thật ngược chiều với vật.
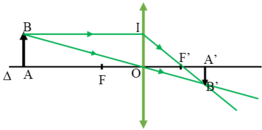
Trên hình vẽ, xét hai cặp tam giác đồng dạng:
ΔABO và ΔA’B’O; ΔA’B’F’ và ΔOIF’.
Từ hệ thức đồng dạng được:![]()
Vì AB = OI (tứ giác BIOA là hình chữ nhật)
![]()
↔ dd' – df = d'f (1)dd' – df = d'f (1)
Chia cả hai vế của (1) cho tích d.d’.f ta được:
![]()
(đây được gọi là công thức thấu kính cho trường hợp ảnh thật)
Thay d = 30cm, f = 15cm ta tính được: OA’ = d’ = 30cm

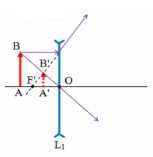
a. Bạn tự vẽ ( ảnh ảo )
b. Xét tam giác \(OAB\sim\) tam giác \(OA'B'\)
\(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}=\dfrac{OI}{A'B'}\) ( do OI = AB ) (1)
Xét tam giác \(OIF'\sim\) tam giác \(A'B'F'\)
\(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'F'}\) (2)
\(\left(1\right);\left(2\right)\Rightarrow\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}=\dfrac{OF'}{OA'+OF'}\)
\(\Leftrightarrow\dfrac{8}{OA'}=\dfrac{12}{OA'+12}\)
\(\Leftrightarrow OA'=24\left(cm\right)\)
Thế \(OA'=24\) vào \(\left(1\right)\Leftrightarrow\dfrac{1}{A'B'}=\dfrac{8}{24}\)
\(\Leftrightarrow A'B'=3\left(cm\right)\)

Chọn đáp án A
Thấu kính vừa cho ảnh thật, vừa cho ảnh ảo => thấu kính hội tụ.
d 1 = 16 c m ; d ' > 0 d > 2 0 ; d ' ' = − 24 c m k 1 = − k 2
⇔ − d ' ' d 2 = d ' d 1 ⇒ d ' . d 2 = − d 1 d ' ' = 384. ⇒ d ' = 384 d 2 ( 1 )
* f = d 1 d ' d 1 + d ' = d 2 d ' ' d 2 + d ' ' ⇔ 16 d ' 16 + d ' = − 24 d 2 d 2 − 24 ( 2 )
( 1 ) , ( 2 ) ⇒ d ' = 48 ( c m ) ⇒ f = 12 ( c m ) .

Chọn đáp án A
Thấu kính vừa cho ảnh thật, vừa cho ảnh ảo => thấu kính hội tụ.
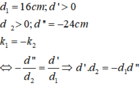
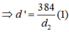
![]()
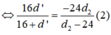
![]()
Đáp án: C
HD Giải:
TKPK cho ảnh ảo:
A’B’ = k. AB = 0,5.2 = 1 cm