Đội tuyển học sinh giỏi của một trường gồm 18 em, trong đó có 7 học sinh khối 12, 6 học sinh khối 11 và 5 học sinh khối10. Hỏi có bao nhiêu cách cử 8 học sinh đi dự đại hội sao cho mỗi khối có ít nhất 1 học sinh được chọn?
A.137123
B.31768
C.37100
D.41811


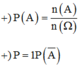
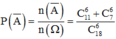
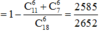
Số cách chọn 8 học sinh gồm hai khối là phần bù của cách chọn 8 học sinh đi dự đại hội sao cho mỗi khối có ít nhất 1 học sinh được chọn.( chú ý mỗi khối đều có ít hơn 8 học sinh).
Số cách chọn 8 học sinh từ hai khối là: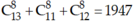 .
.
Số cách chọn 8 học sinh bất kì là: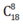
Số cách chọn thỏa yêu cầu bài toán: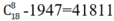
Chọn D.