Cho tập A={1;2;3;4;5;6;7;8;9}. Từ tập A có thể lập được bao nhiêu số tự nhiên chẵn có 3 chữ số đôi một khác nhau sao cho số đó không lớn hơn 788?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1:{2,4};{2,3};{3,4}
2:{a,b,4},...
3:{a},....
------------------------
1 : { 2 ; 4 } ; { 2 ; 3 } ; { 3 ; 4 }
2 : { a , b , 4 } , ........
3 : { a } ,............

Từ biểu diễn của tập hợp B trên trục số, ta có điều kiện cần và đủ để A ⊂ B là
a ; a + 2 ⊂ ( − ∞ ; − 1 ) a ; a + 2 ⊂ ( 1 ; + ∞ ) ⇔ a + 2 < − 1 a > 1 ⇔ a < − 3 a > 1
Vậy tập hợp các giá trị của tham số a sao cho A ⊂ B là ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )
Đáp án A

a, Tập hợp con của A là{1} ,{2}, A,∅
b, Để M ⊂A và M⊂B
thì M={1}
c,Vì A⊂N và B⊂N
Nên N={1;2;4}

ai bao la ko dung thi tim ra cach nhanh nhat de tinh tap con di


Đáp án : A
+) ; c có 4 cách chọn. Chọn chữ số còn lại có 7 cách chọn.
; c có 4 cách chọn. Chọn chữ số còn lại có 7 cách chọn.
+)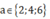 ; c có 3 cách chọn. Chọn chữ số còn lại có 7 cách chọn.
; c có 3 cách chọn. Chọn chữ số còn lại có 7 cách chọn.
+) a = 7;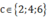 ; b khác 9, b có 6 cách chọn.
; b khác 9, b có 6 cách chọn.
+) a = 7; c = 8; b có 6 cách chọn
Vậy có 3.4.7 + 3.3.7 + 3.6 + 6 = 171 số.