Cho hàm số
y
=
x
-
2
x
+
1
có đồ thị (C) . Phương trình tiếp tuyến
∆
của đồ thị hàm số (C) tạo với hai đường tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất. Khi đó, khoảng cách từ tâm đối xứng của đồ thị đến
∆
bằng?
A
.
3
B
.
2
6
C
.
2
3
...
Đọc tiếp
Cho hàm số y = x - 2 x + 1 có đồ thị (C) . Phương trình tiếp tuyến ∆ của đồ thị hàm số (C) tạo với hai đường tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất. Khi đó, khoảng cách từ tâm đối xứng của đồ thị đến ∆ bằng?
A . 3
B . 2 6
C . 2 3
D . 6
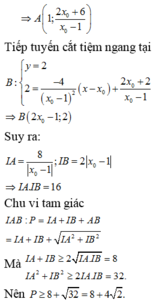
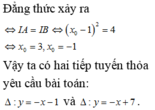
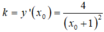
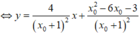
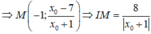
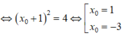
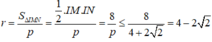
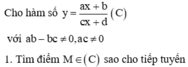
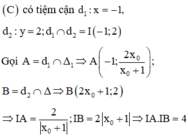
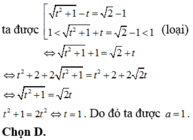
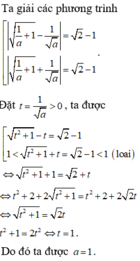
+ Đồ thi hàm số đã cho co TCĐ là : x= -1 và TCN là y= 1; tâm đối xứng- giao của 2 đườg tiệm cận có tọa độ là I ( -1; 1)
Gọi M x 0 ; x 0 - 2 x 0 + 1 ∈ C , x 0 ≠ - 1 , I ( - 1 ; 1 )
+ Phương trình tiếp tuyến tại M có dạng
+ Giao điểm của ∆ với tiệm cận đứng là A - 1 ; x 0 - 5 x 0 + 1
+ Giao điểm của ∆ với tiệm cận ngang là B( 2x0+1; 1).
Ta có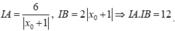
Bán kính đường tròn ngoại tiếp tam giác IAB là S=p.r, suy ra
Suy ra,
Chọn D.