Tính tổng các giá trị của tham số m để đồ thị hàm số: y= - x 4 + 2 m x 2 - 4 m + 1 có ba điểm cực trị . Đồng thời ba điểm cực trị đó cùng với gốc tọa độ tạo thành 1 hình thoi.
A. Không tồn tại m.
B. 2
C. 1/4
D. 9/4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
[Phương pháp tự luận]
Hàm số có 3 điểm cực trị khi m > 0
Ba điểm cực trị là:
![]()
Tứ giác OBAC đã có OB=OC ,AB=AC.
Vậy tứ giác OBAC là hình thoi chỉ cần thêm điều kiện
![]()
![]()
![]()
![]()
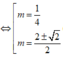 ( thỏa mãn).
( thỏa mãn).

Chọn A
y ' = y = 4 x 3 - 4 m 2 x
Hàm số có 3 điểm cực trị khi m ≠ 0
Khi đó 3 điểm cực trị là
![]()
Gọi I là tâm đường tròn ngoại tiếp( nếu có) của tứ giác ABOC .
Do tính chất đối xứng , ta có
A,O,I thẳng hàng
⇒ A O là đường kính của đường tròn ngoại tiếp( nếu có) của tứ giác ABOC
![]()
![]()
Kết hợp điều kiện m = ± 1 ( thỏa mãn)

Ta có đạo hàm
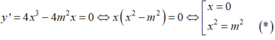
Để hàm số có 3 điểm cực trị khi và chỉ khi m≠0.
Khi đó, tọa độ 3 điểm cực trị là: A( 0; m4+ 3) ; B( m; 3) và C( -m; 3) là ba điểm cực trị.
Vì yA> yB= yC n ên yêu cầu bài toán; tứ giác ABOC nội tiếp đường tròn ( C)
Và A B = A C O B = O C suy ra OA là đường trung trực của đoạn thẳng BC.
Suy ra OA là đường kính của đường tròn C ⇒ O B → . A B → = 0 ( 1 )
Mà ![]()
suy ra 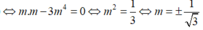
Chọn C.

Chọn A
[Phương pháp trắc nghiệm]
Hàm số có 3 điểm cực trị khi m > 1 3
Áp dụng công thức:
Phương trình đường tròn ngoại tiếp ∆ A B C là:

Thay vào ta có phương trình:
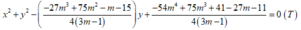
![]()
![]()
Sử dụng chức năng SOLVE ,
tìm ra nghiệm duy nhất thỏa mãn là m = 3

Phương pháp:
+) Tìm tọa độ các điểm cực trị của đồ thị hàm số theo tham số m.
+) Dựa vào tính chất hàm trùng phương và tính chất tứ giác nội tiếp để tìm m.
Cách giải:
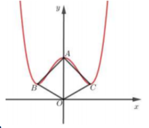

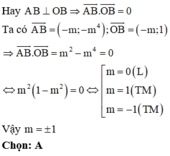

Chọn D
[Phương pháp trắc nghiệm]
Hàm số có 3 điểm cực trị khi m ≠ 0
Áp dụng công thức
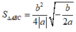
ta có: S ∆ A B C = b 2 4 a - b 2 a
⇔ m = ± 2 5 ( thỏa mãn).

Đáp án C
Phương pháp giải:
Tìm tọa độ các điểm cực trị của hàm số trùng phương sau đó dựa vào tính chất của tứ giác nội tiếp đường tròn để tìm được tham số m
Lời giải:
Ta có



Chọn B
Ta có :
![]()
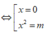
Hàm số đã cho có ba điểm cực trị khi m > 0(*)
Khi đó ba điểm cực trị của đồ thị hàm số là
A ( 0 ; m - 1 ) , B ( - m ; - m 2 + m - 1 )
S ∆ A B C = 1 2 y B - y A x c - x B
![]()
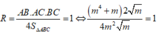
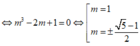
Kết hợp điều kiện (*) ta có
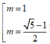
[Phương pháp trắc nghiệm]
Áp dụng công thức
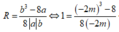
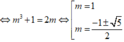
Kết hợp điều kiện (*) ta có
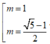

Chọn B
Ta có :
![]()
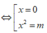
Hàm số đã cho có ba điểm cực trị khi m > 0(*)
Khi đó ba điểm cực trị của đồ thị hàm số là
A ( 0 ; m - 1 ) , B ( - m ; - m 2 + m - 1 )
![]()
S ∆ A B C = 1 2 y B - y A x c - x B
![]()
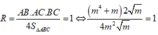
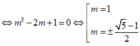
Kết hợp điều kiện (*) ta có
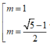
[Phương pháp trắc nghiệm]
Áp dụng công thức
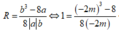
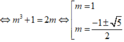
Kết hợp điều kiện (*) ta có
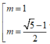
+ Đạo hàm y’ = -4 x3+ 4mx= -4x( x2- m)
Để hàm số có 3 điểm cực trị khi m> 0
+ Tọa độ ba điểm cực trị là: A( 0; 1-4m) ; B ( - m ; m 2 - 4 m + 1 ) ; C ( m ; m 2 - 4 m + 1 )
Tứ giác OBAC đã có OB= OC; AB= AC.
Vậy tứ giác OBAC là hình thoi khi và chỉ khi :
O A = A C h a y ⇔ m + ( m 2 - 4 m + 1 ) 2 = m + m 4 ⇔ ( m 2 - 4 m + 1 ) 2 = m 4
Tổng các giá trị của m thỏa mãn đầu bài là 9/4.
Chọn D.