Hình bên có bao nhiêu góc chung đỉnh O
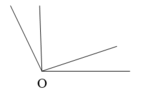
A. 3
B. 4
C. 5
D. 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)Do 5 đường cắt nhau thành 1 điểm thành 10 tia chung góc
Mà 9 tia tạo thành 9 góc
ta có tổng 10 tia nên có số góc là:
9*10=90 góc
Vì mỗi tia đều lặp lại 2 lần nên ta có số góc là:
90:2=45
b) Do 5 đường thẳng cắt nhau tại 1 điểm nên tạo được 5 góc bẹt.
=> có tất cả số khác góc bẹt là: 45-5=40(góc)
Ta có 40 góc khác góc bẹt mà 1 góc là đối đỉnh với nó => số góc đối đỉnh là là: 40:2=20 góc
c) Ta có 5 đường thẳng mà 10 góc ko có điểm nào chung
=> tổng của 10 góc này = 360o
Giả sử cả 10 góc đó < 36o
Mà nếu cả 10 góc đó <36o thì điều này sẽ ko có lý do để cho rằng là đúng
=> Trong tất cả 10 góc đó phải tồn tại 1 góc <36o (đpcm)
Cảm ơn bạn Dante Koryu nha ko ngờ bạn lại hỏi câu mà mình đang muốn hỏi.
Trùng hợp thật.!!!

hình tự vẽ :))
a, 5 đường thẳng đi qua điểm O tạo thành 5 . 2 = 10 (tia)
Cứ 1 tia kết hợp với 9 tia còn lại tạo thành 1 . 9 = 9 (góc)
Nên 10 tia kết hợp với 9 tia còn lại tạo thành 10 . 9 = 90 (góc)
Mà mỗi góc được tính 2 lần
Vậy số góc thực được tạo thành là: 90 : 2 = 45 (góc)
b, 5 đường thẳng tạo thành 5 góc bẹt
Số góc tạo thành không kể góc bẹt là: 45 - 5 = 40 (góc)
Số cặp góc đối đỉnh nhỏ hơn góc bẹt là: 40 : 2 = 20 (cặp)
c. Trong 40 góc nhỏ hơn 180o thì có 10 góc không có điểm trong chung.
Gọi 10 góc đó lần lượt là: \(\widehat{O_1}\); \(\widehat{O_2}\); .... ; \(\widehat{O_{10}}\)
Ta có: \(\widehat{O_1}+\widehat{O_2}+\widehat{O_3}+\widehat{O_4}+\widehat{O_5}=180^o\)
\(\widehat{O_6}+\widehat{O_7}+\widehat{O_8}+\widehat{O_9}+\widehat{O_{10}}=180^o\)
\(\widehat{O_1}+\widehat{O_2}+\widehat{O_3}+\widehat{O_4}+\widehat{O_5}+\widehat{O_6}+\widehat{O_7}+\widehat{O_8}+\widehat{O_9}+\widehat{O_{10}}=180^o+180^o=360^o\)
+) Giả sử: \(\widehat{O_1}=\widehat{O_2}=\widehat{O_3}=....=\widehat{O_{10}}=360^o:10=36^o\)
+) Giả sử 10 góc đều lớn hơn 36o :
\(\Rightarrow\widehat{O_1}+\widehat{O_2}+\widehat{O_3}+\widehat{O_4}+\widehat{O_5}+\widehat{O_6}+\widehat{O_7}+\widehat{O_8}+\widehat{O_9}+\widehat{O_{10}}>360^o\)(Vô lý)
+) Giả sử 10 góc đều nhỏ hơn 36o :
\(\Rightarrow\widehat{O_1}+\widehat{O_2}+\widehat{O_3}+\widehat{O_4}+\widehat{O_5}+\widehat{O_6}+\widehat{O_7}+\widehat{O_8}+\widehat{O_9}+\widehat{O_{10}}< 360^o\)(Vô lý)
Vậy tổng \(\widehat{O_1}+\widehat{O_2}+\widehat{O_3}+\widehat{O_4}+\widehat{O_5}+\widehat{O_6}+\widehat{O_7}+\widehat{O_8}+\widehat{O_9}+\widehat{O_{10}}=360^o\)thì các góc lớn bằng 36o hoặc có ít nhất 1 góc lớn hơn 36o

GIẢI :
a) Năm đường thẳng cắt nhau tại 1 điểm tạo thành 10 tia chung gốc.
Mỗi tia tạo với 9 tia còn lại 9 góc mà có 10 tia như vậy nên có tất cả số góc là:
9 x 10 = 90 góc
Vì mỗi góc được tính lặp lại 2 lần nên có tất cả:
90 : 2 = 45 góc
b) 5 đường thẳng cắt nhau tạo thành 5 góc bẹt. Vậy có tất cả số góc khác góc bẹt là:
45 - 5 = 40 góc khác góc bẹt
Có tất cả 40 góc khác góc bẹt mà mỗi góc có 1 góc đối đỉnh với nó. Nên có tất cả:
40 : 2 = 20 cặp góc đối đỉnh
c) Năm đường thẳng cắt nhau tạo thành 10 góc không có điểm trong chung.
=> Tổng của 10 góc này bằng 360 độ.
Giả sử cả 10 góc đều < 36 độ.
=> Tổng của 10 góc này < 360 độ (Điều này là vô lý)
=> trong 10 góc này tồn tại ít nhất 1 góc nhỏ hơn 36 độ.
Toán lớp 7Hình học
Phạm Diệu Hằng 06/07/2015 lúc 14:29
GIẢI :
a) Năm đường thẳng cắt nhau tại 1 điểm tạo thành 10 tia chung gốc.
Mỗi tia tạo với 9 tia còn lại 9 góc mà có 10 tia như vậy nên có tất cả số góc là:
9 x 10 = 90 góc
Vì mỗi góc được tính lặp lại 2 lần nên có tất cả:
90 : 2 = 45 góc
b) 5 đường thẳng cắt nhau tạo thành 5 góc bẹt. Vậy có tất cả số góc khác góc bẹt là:
45 - 5 = 40 góc khác góc bẹt
Có tất cả 40 góc khác góc bẹt mà mỗi góc có 1 góc đối đỉnh với nó. Nên có tất cả:
40 : 2 = 20 cặp góc đối đỉnh
c) Năm đường thẳng cắt nhau tạo thành 10 góc không có điểm trong chung.
=> Tổng của 10 góc này bằng 360 độ.
Giả sử cả 10 góc đều < 36 độ.
=> Tổng của 10 góc này < 360 độ (Điều này là vô lý)
=> trong 10 góc này tồn tại ít nhất 1 góc nhỏ hơn 36 độ.
Đáp án D