rút gọn: a3 + 2a2 - 1 / a3 - 2a2 - 2a +1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 7 2021
Xét hiệu \(2a^2+2b^2-\left(a^3+ab^2\right)=\left(2a^2-a^3\right)+\left(2b^2-ab^2\right)\)
\(=a^2\left(2-a\right)+b^2\left(2-a\right)\)
\(=\left(a^2+b^2\right)\left(2-a\right)\)
Do \(a^2+b^2\ge0;\forall a;b\) nên:
\(2a^2+2b^2>a^3+ab^2\) khi \(\left\{{}\begin{matrix}a^2+b^2\ne0\\2-a>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a^2+b^2\ne0\\a< 2\end{matrix}\right.\)
\(2a^2+2b^2=a^3+ab^2\) khi \(\left[{}\begin{matrix}a^2+b^2=0\\2-a=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}a=b=0\\a=2\end{matrix}\right.\)
\(2a^2+2b^2< a^3+ab^2\) khi \(\left\{{}\begin{matrix}a^2+b^2\ne0\\a>2\end{matrix}\right.\) \(\Rightarrow a>2\)
\(2a^2+2b^2\ge a^3+ab^2\) khi \(2-a\ge0\Leftrightarrow a\le2\)
9 tháng 9 2023
1: \(=\dfrac{-\left[\left(x+5\right)^2-9\right]}{\left(x+2\right)^2}=\dfrac{-\left(x+5-3\right)\left(x+5+3\right)}{\left(x+2\right)^2}\)
\(=\dfrac{-\left(x+2\right)\left(x+8\right)}{\left(x+2\right)^2}=\dfrac{-\left(x+8\right)}{x+2}\)
2: \(=\dfrac{2x\left(x^2-4x+16\right)}{\left(x+4\right)\left(x^2-4x+16\right)}=\dfrac{2x}{x+4}\)
3: \(=\dfrac{5x\left(x^2+1\right)}{\left(x^2-1\right)\left(x^2+1\right)}=\dfrac{5x}{x^2-1}\)
4: \(=\dfrac{3\left(x^2-4x+4\right)}{x\left(x^3-8\right)}=\dfrac{3\left(x-2\right)^2}{x\left(x-2\right)\left(x^2+2x+4\right)}\)
\(=\dfrac{3\left(x-2\right)}{x\left(x^2+2x+4\right)}\)
5: \(=\dfrac{2a\left(a-b\right)}{a\left(c+d\right)-b\left(c+d\right)}=\dfrac{2a\left(a-b\right)}{\left(c+d\right)\left(a-b\right)}=\dfrac{2a}{c+d}\)
6: \(=\dfrac{x\left(x-y\right)}{\left(x-y\right)\left(x+y\right)}\cdot\left(-1\right)=\dfrac{-x}{x+y}\)
7: \(=\dfrac{2\left(1-a\right)}{-\left(1-a^3\right)}=\dfrac{-2\left(1-a\right)}{\left(1-a\right)\left(1+a+a^2\right)}=-\dfrac{2}{1+a+a^2}\)
8: \(=\dfrac{x^4\left(x^3-1\right)}{\left(x^3-1\right)\left(x^3+1\right)}=\dfrac{x^4}{x^3+1}\)
9: \(=\dfrac{\left(x+2-x+2\right)\left(x+2+x-2\right)}{16x}=\dfrac{4\cdot2x}{16x}=\dfrac{1}{2}\)
10: \(=\dfrac{0.5\left(49x^2-y^2\right)}{0.5x\left(7x-y\right)}=\dfrac{1}{x}\cdot\dfrac{\left(7x-y\right)\left(7x+y\right)}{7x-y}\)
\(=\dfrac{7x+y}{x}\)
11 tháng 7 2021
a) Ta có: \(a^2+2a-4=0\)
\(\Leftrightarrow\left(\sqrt{5}-1\right)^2+2\left(\sqrt{5}-1\right)-4=0\)
\(\Leftrightarrow6-2\sqrt{5}+2\sqrt{5}-2-4=0\)
\(\Leftrightarrow0=0\)(đúng)
b) Ta có: \(\left(a^3+2a^4-4a+2\right)^{10}\)
\(=\left[a\left(a^2+2a-4\right)+2\right]^{10}\)
\(=2^{10}=1024\)
CM
3 tháng 10 2018
a) Ta có x 6 + 2 x 3 + 3 x 3 − 1 . 3 x x + 1 . x 2 + x + 1 x 6 + 2 x 3 + 3 = 3 x x 2 − 1
b) Gợi ý: a 3 + 2 a 2 - a - 2 = (a - 1)(a + 1) (a + 2)
Thực hiện phép tính từ trái qua phải thu được: = 1 3
CM
25 tháng 12 2018
Chọn D.
Phương pháp:
Đạo hàm hàm số f(x) và chọn giá trị x phù hợp để tính giá trị biểu thức đề bài cho.
CM
18 tháng 3 2017
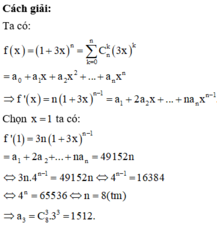
Chọn D
Đạo hàm hai vế f(x)
Số hạng tổng quát thứ k + 1 trong khai triển thành đa thức của 
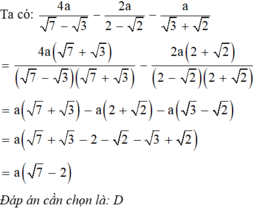
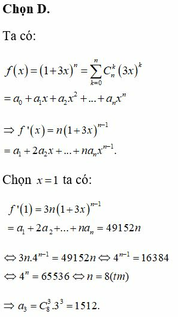
Lời giải:
$\frac{a^3+2a^2-1}{a^3-2a^2-2a+1}$
$=\frac{(a^3+a^2)+(a^2-1)}{(a^3+a^2)-(3a^2+3a)+(a+1)}$
$=\frac{a^2(a+1)+(a+1)(a-1)}{a^2(a+1)-3a(a+1)+(a+1)}$
$=\frac{(a+1)(a^2+a-1)}{(a+1)(a^2-3a+1)}$
$=\frac{a^2+a-1}{a^2-3a+1}$