Tìm giá trị của a để 101a chia hết cho 11
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


76a23 chia hết cho 9
=> 7 + 6 + 2 + 3 + a chia hết cho 9
=> 18 + a chia hết cho 9
=> a = 0 hoặc a = 9
b) có nếu a = 9
~ hok tốt ~
a)
Để 76a23 chia hết cho 9 thì
7 + 6 + a + 2 + 3 chia hết cho 9
hay 18 + a chia hết cho a
=> a = { 0; 9 }
b)
Lần lượt thay a vào số đó ta thấy a = 9 thì 76a23 chia hết cho 11

76a23 chia hết cho 9
=> 7 + 6 + 2 + 3 + a chia hết cho 9
=> 18 + a chia hết cho 9
=> a = 0 hoặc a = 9
b) có nếu a = 9

Bài 3:
Ta có: \(2n^2+n-7⋮n-2\)
\(\Leftrightarrow2n^2-4n+5n-10+3⋮n-2\)
\(\Leftrightarrow n-2\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{3;1;5;-1\right\}\)

\(a,n^3-2n^2+3n+3=n^3-n^2-n^2+n+2n-2+5\\ =\left(n-1\right)\left(n^2-n+2\right)+5\\ \Leftrightarrow n^3-2n^2+3n+3⋮\left(n-1\right)\\ \Leftrightarrow5⋮n-1\\ \Leftrightarrow n-1\in\left\{-5;-1;1;5\right\}\\ \Leftrightarrow n\in\left\{-4;0;2;6\right\}\)
\(b,\Leftrightarrow x^4+6x^3+7x^2-6x+a\\ =x^4+3x^3-x^2+3x^3+9x^2-3x-x^2-3x+1-1+a\\ =\left(x^2+3x-1\right)\left(x^2+3x-1\right)-1+a\\ =\left(x^2+3x-1\right)^2+a-1\)
Để \(x^4+6x^3+7x^2-6x+a⋮x^2+3x-1\)
\(\Leftrightarrow a-1=0\Leftrightarrow a=1\)
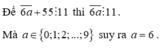
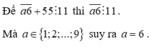
Để 101 a ⋮ 11 thì a ⋮ 11