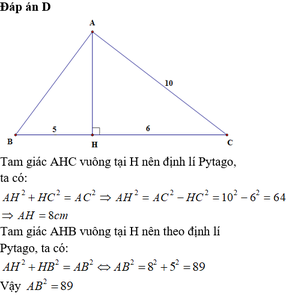
Cho tam giác ABC có các góc B,C nhọn. Kẻ AH ⊥ BC. Biết AC = 10cm, HB = 5cm, HC = 6cm. Tính A B 2
A. 100
B. 61
C. 64
D. 89
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm

Áp dụng định lý Pi ta go, ta có:
AH2 + HC2 = AC2
<=> AH2 = AC2 - HC2
<=> AH2 = 152 - 92
<=> AH2 = 144
Áp dụng định lý Pi ta go, ta có:
AB2 = AH2 + BH2
<=> AB2 = 144 + 52
<=> AB2 = 144 + 25
<=> AB2 = 169
=> \(AB=\sqrt{169}=13\)
=> AB = 13 cm
nha
Bạn tự vẽ hình nhé.
Xét tam giác AHC vuông tại H có: AC2 = AH2 + HC2 (Định lí Pitago)
=> 152 = AH2 + 92
=> AH2 = 144
Xét tam giác AHB vuông tại H có AB2 = AH2 + HB2 (Định lí Pitago)
=> AB2 = 144 + 52
=> AB2 = 169
=> AB = 13 (cm)

HB=HC
AH CẠNH CHUNG
AB=AC (CẠNH HUYỀN)
DO ĐÓ:AHB=AHC (C-C-C)
MÌNH LÀM ĐC NHIU ĐÓ CÒN NHIU BN TỰ LÀM NHÉ!!!

Bạn ơi, mình sắp xếp các cạnh và các góc đúng, không sai đâu nên đừng viết ngược lại nhá
a, Ta có : BH = HC = BC : 2
=> BH = HC = 8 : 2
=> BH = HC = 4 ( cm )
=> BH = HC
b, - Xét tam giác AHB vuông tại H có :
AC2 = AH2 + HC2
=> 52 = AH2 + 42
=> 25 = AH2 + 16
=> AH2 = 25 + 16
=> AH2 = 41
=> AH = 20,5 ( cm )

b) Xét ΔABH vuông tại H và ΔCBA vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔABH\(\sim\)ΔCBA(g-g)
Suy ra: \(\dfrac{AB}{CB}=\dfrac{HB}{AB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=BC\cdot BH\)(đpcm)
Có gấp thế nào đi nữa thì phải đủ dữ kiện đề tụi tớ mới giúp được cậu nhé :))