Cho tam giác ABC có M là trung điểm của BC và AM là tia phân giác của góc A. Khi đó, tam giác ABC là tam giác gì?
A. △ B A C cân tại B
B. △ B A C cân tại B
C. △ B A C đều
D. △ B A C cân tại B
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
20 tháng 6 2018
Đúng(0)
Những câu hỏi liên quan
9 tháng 5 2021
b) Ta có: G là trọng tâm của ΔBAC(gt)
mà AM là đường trung tuyến ứng với cạnh BC(M là trung điểm của BC)
nên \(AM=\dfrac{3}{2}\cdot AG\)(Định lí)
\(\Leftrightarrow AM=\dfrac{3}{2}\cdot4=6\left(cm\right)\)
Ta có: ΔABC cân tại A(cmt)
mà AM là đường trung tuyến ứng với cạnh đáy BC(M là trung điểm của BC)
nên AM là đường cao ứng với cạnh BC(Định lí tam giác cân)
Ta có: M là trung điểm của BC(gt)
nên \(BM=CM=\dfrac{BC}{2}=\dfrac{16}{2}=8\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABM vuông tại M, ta được:
\(AB^2=AM^2+BM^2\)
\(\Leftrightarrow AB^2=6^2+8^2=100\)
hay AB=10(cm)
Vậy: AM=6cm; AB=10cm
9 tháng 5 2021
a) Xét ΔABC có:
AM là đường trung tuyến ứng với cạnh BC(M là trung điểm của BC)
AM là đường phân giác ứng với cạnh BC(Gt)
Do đó: ΔABC cân tại A(Định lí tam giác cân)
Y
29 tháng 4 2016
5 )
tự vẽ hình nha bạn
a)
Xét tam giác ABM và tam giác ACM có :
AM cạnh chung
AB = AC (gt)
BM = CM (gt)
suy ra : tam giác ABM = tam giác ACM ( c-c-c)
suy ra : góc BAM = góc CAM ( 2 góc tương ứng )
Hay AM là tia phân giác của góc A
b)
Xét tam giác ABD và tam giác ACD có :
AD cạnh chung
góc BAM = góc CAM ( c/m câu a)
AB = AC (gt)
suy ra tam giác ABD = tam giác ACD ( c-g-c)
suy ra : BD = CD ( 2 cạnh tương ứng)
C) hay tam giác BDC cân tại D
XT
30 tháng 4 2016
Bài 4: a) Xét ABE vàHBE có:
BE chung
ABE= EBH (vì BE là phân giác)
=> ABE=HBE (cạnh huyền- góc nhọn)
b, Vì ABE=HBE(cmt)
=> BA = BH và EA = EH
=> điểm B, E cách đều 2 mút của đoạn thẳng AH
=>BE là đường trung trực của đoạn thẳng AH
c, Vì AC vuông góc BK => EAK = \(90\) độ
EH vuông góc BC => EHC = 90 độ
Xét AEK vàHEC có:
EAK = EHC (= 90độ)(cmt)
AE = EH (cmt)
AEK = HEC (đối đỉnh)
=> AEK HEC (g.c.g)
=> EK = EC (2 cạnh tương ứng)
Xét HEC vuông tại H (vì EHC = 90 độ )
có EH < EC(cạnh huyền lớn hơn cạnh góc vuông)
Mà AE = EH (cmt) => AE < EC
30 tháng 4 2016
Bạn tự vẽ hình nha!!!
3a.
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
ABD = EBD (BD là tia phân giác của ABE)
BD là cạnh chung
=> Tam giác ABD = Tam giác EBD (cạnh huyền - góc nhọn)
=> AB = EB (2 cạnh tương ứng) => B thuộc đường trung trực của AE
=> AD = ED (2 cạnh tương ứng) => D thuộc đường trung trực của AE
=> BD là đường trung trực của AE.
3b.
Xét tam giác AFD và tam giác ECD có:
FAD = CED ( = 90 )
AD = ED (tam giác ABD = tam giác EBD)
ADF = EDC (2 góc đối đỉnh)
=> Tam giác ADF = Tam giác EDC (g.c.g)
=> DF = DC (2 cạnh tương ứng)
3c.
Tam giác ADF vuông tại A có:
AD < FD (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà FD = CD (theo câu b)
=> AD < CD.
VN
30 tháng 4 2016
3a.
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
ABD = EBD (BD là tia phân giác của ABE)
BD là cạnh chung
=> Tam giác ABD = Tam giác EBD (cạnh huyền - góc nhọn)
=> AB = EB (2 cạnh tương ứng) => B thuộc đường trung trực của AE
=> AD = ED (2 cạnh tương ứng) => D thuộc đường trung trực của AE
=> BD là đường trung trực của AE.
3b.
Xét tam giác AFD và tam giác ECD có:
FAD = CED ( = 90 )
AD = ED (tam giác ABD = tam giác EBD)
ADF = EDC (2 góc đối đỉnh)
=> Tam giác ADF = Tam giác EDC (g.c.g)
=> DF = DC (2 cạnh tương ứng)
3c.
Tam giác ADF vuông tại A có:
AD < FD (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà FD = CD (theo câu b)
=> AD < CD.
30 tháng 1 2021
a) Ta có: \(\widehat{ABC}+\widehat{MBC}=\widehat{ABM}\)(tia BC nằm giữa hai tia BA,BM)
nên \(\widehat{ABC}+\widehat{MBC}=90^0\)(1)
Ta có: \(\widehat{ACB}+\widehat{MCB}=\widehat{ACM}\)(tia CB nằm giữa hai tia CA,CM)
nên \(\widehat{ACB}+\widehat{MCB}=90^0\)(2)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)(3)
Từ (1), (2) và (3) suy ra \(\widehat{MBC}=\widehat{MCB}\)
Xét ΔMBC có \(\widehat{MBC}=\widehat{MCB}\)(cmt)
nên ΔMBC cân tại M(Định lí đảo của tam giác cân)
b) Xét ΔABM vuông tại B và ΔACM vuông tại C có
AB=AC(ΔABC cân tại A)
BM=CM(ΔMBC cân tại M)
Do đó: ΔABM=ΔACM(hai cạnh góc vuông)
⇒\(\widehat{BAM}=\widehat{CAM}\)(hai góc tương ứng)
mà tia AM nằm giữa hai tia AB,AC
nên AM là tia phân giác của \(\widehat{BAC}\)(đpcm)
Ta có: ΔABM=ΔACM(cmt)
nên \(\widehat{BMA}=\widehat{CMA}\)(hai góc tương ứng)
mà tia MA nằm giữa hai tia MB,MC
nên MA là tia phân giác của \(\widehat{BMC}\)(đpcm)
c) Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)
Ta có: MB=MC(ΔMBC cân tại M)
nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(5)
Từ (4) và (5) suy ra AM là đường trung trực của BC
hay AM⊥BC(đpcm)
12 tháng 5 2023
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
b: ΔABD=ΔACE
=>AD=AE
=>ΔADE cân tại A
c: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
ΔADE cân tại A
mà AM vuông góc DE
nên AM là phân giác của góc DAE
d: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH=góc CAK
=>ΔAHB=ΔAKC
=>AH=AK
=>ΔAHK cân tại A
21 tháng 9 2023
Tham khảo:
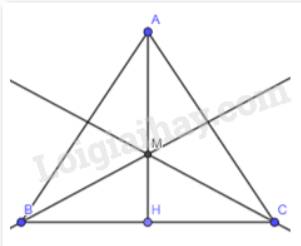
Vì M là giao điểm của 2 phân giác góc B, C nên M là điểm giao của 3 phân giác trong tam giác ABC
\( \Rightarrow \) AM cũng là phân giác của góc A (định lí về 3 phân giác cùng đi qua 1 điểm)
\( \Rightarrow \widehat {BAH} = \widehat {CAH}\)(tính chất tia phân giác của 1 góc)
Xét tam giác ABH và tam giác ACH có :
AB = AC ( tam giác ABC cân tại A )
\(\widehat {BAH} = \widehat {CAH}\)(chứng minh trên)
AH cạnh chung
\( \Rightarrow \DeltaABH=\Delta ACH\) (c.g.c)
\( \Rightarrow \) HB = HC (cạnh tương ứng) \( \Rightarrow \)H là trung điểm của BC