Một máy bay đang bay ở độ cao 1700m. Từ một đài quan sát ở mặt đất người ta nhìn thấy máy bay dưới một góc 250 so với mặt đất. Hãy tính khoảng cách từ đài quan sát đến máy bay? (Làm tròn đến mét)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 8 2018
Độ cao của máy bay là CD, độ dài AB = 60m; D A C ^ = 30 0 ; D B C ^ = 50 0
Gọi BC = x => AC = 60 + x
Xét tam giác BDC vuông tại C có:
Xét tam giác ADC vuông tại C có:
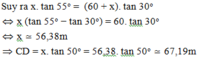
Vậy độ cao của máy bay so với mặt đất là 67,19m
Đáp án cần chọn là: C
CM
28 tháng 1 2019
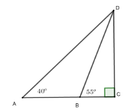
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
Đáp án cần chọn là: A
3 tháng 8 2021
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
2 tháng 12 2023
Gọi C là vị trí của máy bay
Gọi CH là độ cao của máy bay so với mặt đất
=>CH\(\perp\)AB tại H
Ta có hình vẽ sau:
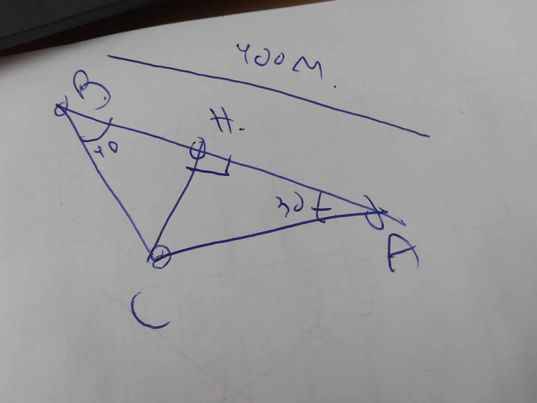
Xét ΔCBA có \(\widehat{CBA}+\widehat{CAB}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+30^0+40^0=180^0\)
=>\(\widehat{ACB}=110^0\)
Xét ΔABC có \(\dfrac{BA}{sinACB}=\dfrac{AC}{sinB}=\dfrac{BC}{sinA}\)
=>\(\dfrac{400}{sin110}=\dfrac{AC}{sin40}=\dfrac{BC}{sin30}\)
=>\(AC\simeq273,62\left(m\right);BC\simeq212,84\left(m\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinACB\)
\(=\dfrac{1}{2}\cdot273,62\cdot212,84\cdot sin110\simeq27362,57\left(m^2\right)\)
Xét ΔACB có CH là đường cao
nên \(\dfrac{1}{2}\cdot CH\cdot AB=S_{ABC}\)
=>\(CH\cdot\dfrac{400}{2}=27362,57\)
=>\(CH\simeq136,81\left(m\right)\)
CM
26 tháng 6 2018
Chọn C.
Phương pháp:
Gắn hệ trục tọa độ, xác định tọa độ điểm M trên parabol y = x 2 để độ dài đoạn AM nhỏ nhất.
Cách giải:
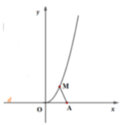
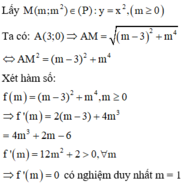
Ta có bảng biến thiên sau:
1 tháng 8 2023
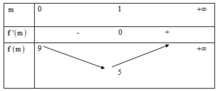
Gọi giao điểm của đường nhìn thấy máy bay tại A và B là C.
Vẽ CH vuông góc AB
=>CH là độ cao của máy bay
góc ACB=180-40-32=108 độ
Xét ΔACB có
AB/sin C=AC/sinB=BC/sin A
=>400/sin108=AC/sin32=BC/sin40
=>\(AC\simeq222,9\left(m\right);BC\simeq270,3\left(m\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinC=\dfrac{1}{2}\cdot222.9\cdot270.3\cdot sin108\simeq28650,52\left(m^2\right)\)
Độ cao là:"
28650,52*2/400\(\simeq143\left(m\right)\)
K/c là \(\dfrac{1700}{\sin25^0}\approx4023\left(m\right)\)