Cho ΔABC, AE là phân giác ngoài của góc A. Hãy chọn câu đúng:
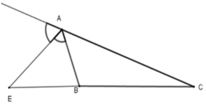
A. A B A E = B E C E
B. A E A C = B E C E
C. A B A C = C E B E
D. A B A C = B E C E
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AC=AD+DC
=3+5
=8(cm)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{AB}{AD}=\dfrac{CB}{CD}\)
=>\(\dfrac{AB}{3}=\dfrac{CB}{5}=k\)
=>AB=3k; CB=5k
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(\left(5k\right)^2=\left(3k\right)^2+8^2\)
=>\(16k^2=64\)
=>\(k^2=4\)
=>k=2
=>AB=3*2=6cm; BC=2*5=10(cm)
b: Xét ΔBAC có BE là phân giác góc ngoài tại B
nên \(\dfrac{EA}{EC}=\dfrac{BA}{BC}\)
=>\(\dfrac{EA}{EC}=\dfrac{3}{5}\)
=>\(\dfrac{EA}{3}=\dfrac{EC}{5}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{EC}{5}=\dfrac{EA}{3}=\dfrac{EC-EA}{5-3}=\dfrac{AC}{2}=\dfrac{8}{2}=4\)
=>EA=12(cm)

a. hạ đương cao AK
suy ra BK=KC=3:2=1.5(cm)
Xét tam giac ABC có góc AKB=90
AK^2+BK^2=AB^2(đl py-ta-go)
AK=\(\dfrac{3\sqrt{3}}{2}\)
SABC=\(\dfrac{1}{2}.\dfrac{3\sqrt{3}}{2}.3=\dfrac{9\sqrt{3}}{4}\)

Vì trong tam giác, đường phân giác của một góc chia cạnh đối diện thanh hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy nên A B A C = B E C E
A B A C = B E C E ⇒ A B B E = A C C E nên C đúng
A B B E = A C C E ⇒ C E A C = B E A B nên A đúng
Chỉ có B sai.
Đáp án: B

\(\text{#TNam}\)
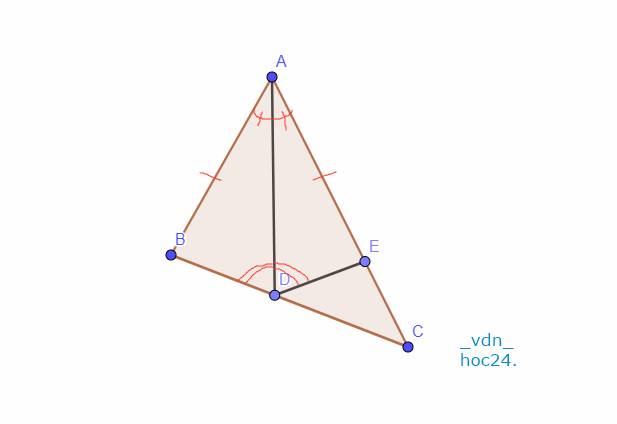
`a,` \(\text{Xét Tam giác ABD và Tam giác AED có:}\)
`AB = AE (g``t)`
\(\widehat{BAD}=\widehat{EAD} (\text {tia phân giác} \) \(\widehat{BAE})\)
`\text {AD chung}`
`=> \text {Tam giác ABD = Tam giác AED (c-g-c)}`
`b,`
\(\text{Vì Tam giác ABD = Tam giác AED (a)}\)
`->`\(\widehat{ADB}=\widehat{ADE} (\text {2 góc tương ứng})\)
`-> \text {AD là tia phân giác}` \(\widehat{BDE}\)
\(\text{Xét Tam giác ABC:}\)
`AC > AB (g``t)`
\(\text{Theo định lý của quan hệ giữa góc và cạnh đối diện trong 1 tam giác}\)
`->`\(\widehat{ABC}>\widehat{ACB}.\)
Vì trong tam giác, đường phân giác của một góc chia cạnh đối diện thanh hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy nên A B A C = B E C E
Đáp án D