Cho ΔABC vuông tại A có góc C = 60 độ , AB= \(\sqrt{192}\)cm.
Diện tích của ΔABC là \(\sqrt{a}\).cm Vậy a =
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 1 2016
Kẻ AH vuông góc với BC
Có: A + B + C = 1800 => B = 180 - (A + C) = 180- (90 - 60) = 300
Trong tam giác AHB có: AH là đường cao và góc ABH = 300
=> tam giác AHB là 1/2 tam giác đều
=> BH = \(\frac{AB\sqrt{3}}{2}=\frac{\sqrt{192}.\sqrt{3}}{2}=12cm\)
và AH = 1/2.AB = 1/2.\(\sqrt{192}\) = \(4\sqrt{3}cm\)
Có: AH2 = HB.HC => HC = \(\frac{AH^2}{HB}=\frac{\left(4\sqrt{3}\right)^2}{12}=4cm\)
=> BC = HB + HC = 12 + 4 = 16cm
Diên tích của tam giác ABC: \(S_{ABC}=\frac{AH.BC}{2}=\frac{4\sqrt{3}.16}{2}=32\sqrt{3}cm^2=\sqrt{a}\Rightarrow a=\left(32\sqrt{3}\right)^2=3072\)
Vậy a = 3072
2 tháng 10 2021
Bài 1:
a: Xét ΔBAC vuông tại A có
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔBAC vuông tại A có
\(AB=BC\cdot\sin60^0\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow AC=2\sqrt{3}\left(cm\right)\)
2 tháng 10 2021
Bài 2:
b: \(AH\cdot\left(\cot\widehat{B}+\cot\widehat{C}\right)\)
\(=AH\cdot\left(\dfrac{BH}{AH}+\dfrac{CH}{AH}\right)\)
\(=AH\cdot\dfrac{BC}{AH}=BC\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2023
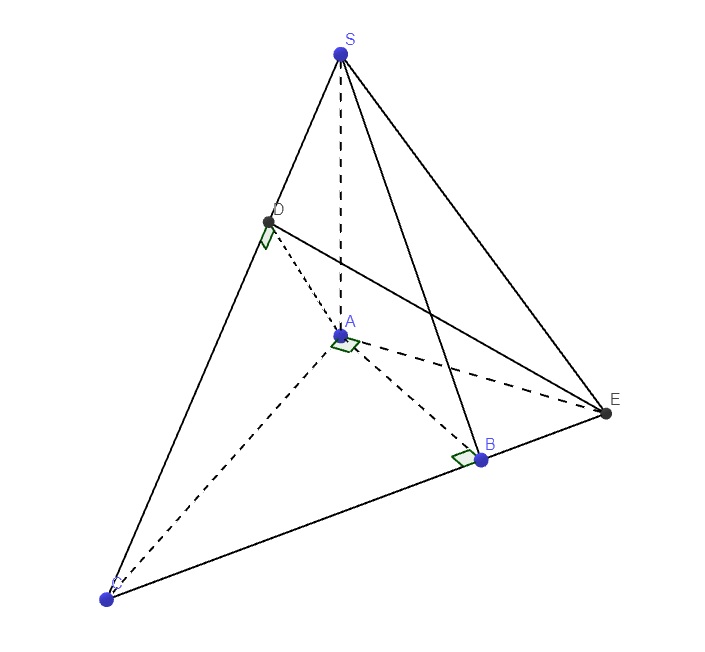
Trong mp (SAC), từ A kẻ \(AD\perp SC\) (D thuộc SC) (1)
Trong mp (ABC), qua A kẻ đường thẳng vuông góc AC cắt BC kéo dài tại E
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp AE\\AE\perp AC\end{matrix}\right.\) \(\Rightarrow AE\perp\left(SAC\right)\Rightarrow\left\{{}\begin{matrix}AE\perp AE\\AE\perp SC\left(2\right)\end{matrix}\right.\)
(1);(2) \(\Rightarrow SC\perp\left(ADE\right)\)
Mà \(SC=\left(SAC\right)\cap\left(SBC\right)\Rightarrow\widehat{ADE}\) là góc giữa (SAC) và (SBC)
\(AC=\sqrt{AB^2+BC^2}=2a\)
Hệ thức lượng: \(\dfrac{1}{AD^2}=\dfrac{1}{SA^2}+\dfrac{1}{AC^2}\Rightarrow AD=\dfrac{2a\sqrt{33}}{11}\)
\(\dfrac{1}{AB^2}=\dfrac{1}{AC^2}+\dfrac{1}{AE^2}\Rightarrow AE=\dfrac{AB.AC}{\sqrt{AC^2-AB^2}}=\dfrac{2a\sqrt{3}}{3}\)
\(\Rightarrow tan\widehat{ADE}=\dfrac{AE}{AD}=...\)
