Cho hình chóp S.ABC có tam giác ABC là tam giác vuông cân tại S, SB = 2a và khoảng cách từ A đến mặt phẳng (SBC) bằng 3a. Tính theo a thể tích V của khối chóp S.ABC
A. V = 2 a 3
B. V = 4 a 3
C. V = 6 a 3
D. V = 12 a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Ta chọn (SBC) làm mặt đáy => chiều cao khối chóp là
![]()
Tam giác SBC vuông cân tại S nên
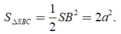
Vậy thể tích khối chóp
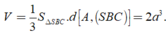

Hạ \(SH\perp BC\Rightarrow\left(SBC\right)\perp\left(ABC\right)\)
\(\Rightarrow SH\perp BC;SH=SB.\sin\widehat{SBC}=a\sqrt{3}\)
Diện tích : \(S_{ABC}=\frac{12}{\boxtimes}BA.BC=6a^2\)
Thể tích : \(V_{s.ABC}=\frac{1}{3}S_{ABC}.SH=2a^3\sqrt{3}\)
Hạ \(HD\perp AC\left(D\in AC\right),HK\perp SD\left(K\in SD\right)\)
\(\Rightarrow HK\perp\left(SAC\right)\Rightarrow HK=d\left(H,\left(SAC\right)\right)\)
\(BH=SB.\cos\widehat{SBC}=3a\Rightarrow BC=4HC\)
\(\Rightarrow d\left(B,\left(SAC\right)\right)=4d\left(H,SAC\right)\)
Ta có : \(AC=\sqrt{BA^2+BC^2}=5a;HC=BC-BH=a\)
\(\Rightarrow HD=BA.\frac{HC}{AC}=\frac{3a}{5}\)
\(HK=\frac{SH.HS}{\sqrt{SH^2+HD^2}}=\frac{3a\sqrt{7}}{14}\)
Vậy \(d\left(B,\left(SAC\right)\right)=4HK=\frac{6a\sqrt{7}}{7}\)

Đáp án A
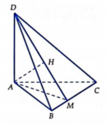
Trong mặt phẳng (ABC) Kẻ A M ⊥ B C
Trong mặt phẳng (SAM) kẻ A H ⊥ S M
⇒ d A ; S B C = A H
Ta có A M = A B . cos B A M ^ = A B . cos 60 0 = a 2
Diện tích tam giác ABC là S A B C = 1 2 A B . A C . sin 120 0 = 1 2 a 2 3 2 = a 2 3 4 Ta có
V S . A B C = 1 3 . S A . S A B C = 1 3 . S A . a 3 3 24 = a 3 3 24 ⇒ S A = a 2
Tam giác SAM vuông tại A có AH là đường cao
⇒ 1 A H 2 = 1 S A 2 + 1 A M 2 ⇒ A H = a 2 4
Ta chọn (SBC) làm mặt đáy => chiều cao khối chóp là d(A, (SBC)) = 3a
Tam giác SBC vuông cân tại S nên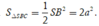
Vậy thể tích khối chóp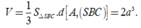
Chọn A.