Một nhà máy sản xuất nước ngọt cần làm các lon dựng dạng hình trụ với thể tích đựng được là V. Biết rằng diện tích toàn phần nhỏ nhất thì tiết kiệm chi phí nhất. Tính bán kính của lon để tiết kiệm chi phí nhất
A. V 2 π 3
B. V 3 π 3
C. V 4 π 3
D. V π 3

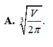
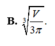
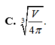
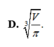


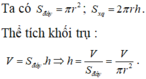
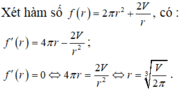
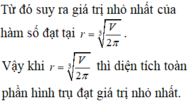
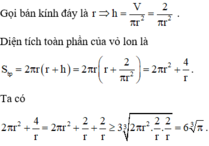
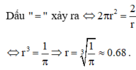

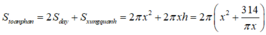
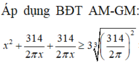
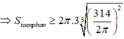
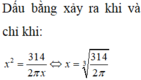

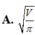
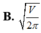
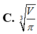
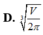


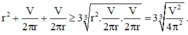
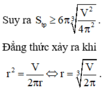
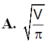
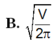
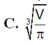
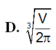
Gọi bán kính hình trụ là x > 0.
Khi đó ta có diện tích của hai đáy thùng là S 1 = 2 πx 2 Diện tích xung quanh của thùng là S 2 = 2 πxh = 2 πx V πx 2 = 2 V x
trong đó h là chiều cao của thùng và từ V = πx 2 . h ⇒ h = V πx 2
Vậy diện tích toàn phần của thùng là S = S 1 + S 2 = 2 πx 2 + 2 V x
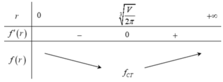
Để tiết kiệm vật liệu nhất thì S phải bé nhất. Áp dụng bất đẳng thức AM-GM ta có
S = 2 πx 2 + V 2 x + V 2 x ≥ 2 . 3 πV 2 4 3
Do đó S bé nhất khi và chỉ khi πx 2 = V 2 x ⇔ x = V 2 π 3
Đáp án A