Rút gọn biểu thức 6 x 2 y ( x 2 ) 8 x 3 y 2 x 2 3 x 2...

PT

Pham Trong Bach

18 tháng 12 2018

Rút gọn biểu thức 6 x 2 y ( x + 2 ) 8 x 3 y 2 x 2 + 3 x + 2 A. - 3 4 x y ( x + 1 ) B. 3 4 x y ( x + 1 ) C. x 4 x y ( x + 1 ) D. 6 ...

Đọc tiếp

#Toán lớp 8

1

CM

Cao Minh Tâm

18 tháng 12 2018

Đúng(0)

LH

Lê Hoàng Thùy Linh

19 tháng 10 2023 - olm

Rút gọn rồi tính giá trị của biểu thức

a)M=(x^2+3xy-3x^3)+(2y^3-xy+3x^3)-y^3 tại x=5 và y=4

b) N= x^2(x+y)-y(x^2-y^2) tại x=-6 y=8

c)P=x^2+1/2x+1/16 biết x= 3/4

#Toán lớp 8

1

KV

Kiều Vũ Linh

19 tháng 10 2023

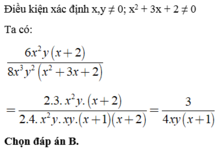
a) M = (x² + 3xy - 3x³) + (2y³ - xy + 3x³)

= x² + 3xy - 3x³ + 2y³ - xy + 3x³

= x² + (3xy - xy) + (-3x³ + 3x³) + 2y³

= x² + 2xy + 2y³

Tại x = 5 và y = 4

M = 5² + 2.5.4 + 2.4³

= 25 + 40 + 2.64

= 65 + 128

= 193

b) N = x²(x + y) - y(x² - y²)

= x³ + x²y - x²y + y³

= x³ + (x²y - x²y) + y³

= x³ + y³

Tại x = -6 và y = 8

N = (-6)³ + 8³

= -216 + 512

= 296

c) P = x² + 1/2 x + 1/16

= (x + 1/2)²

Tại x = 3/4 ta có:

P = (3/4 + 1/2)² = (5/4)² = 25/16

Đúng(1)

N

Nguyenngocdiem

29 tháng 6 2023

Bài 3: Rút gọn biểu thức (Dùng hằng đẳng thức)1, (x+y)$^2$-(x-y)$^2$2, (x+y)$^3$-(x-y)$^3$-2y$^3$3,(x+y)$^2$-2(x+y)(x-y)+(x-y)$^2$4,(2x+3)$^2$-2(2x+3)(2x+5)+(2x+5)$^2$5, 9$^8$....

Đọc tiếp

#Toán lớp 8

2

Y

YangSu

29 tháng 6 2023

$1,\left(x+y\right)^2-\left(x-y\right)^2=\left[\left(x+y\right)-\left(x-y\right)\right]\left[\left(x+y\right)+\left(x-y\right)\right]=\left(x+y-x+y\right)\left(x+y+x-y\right)=2y.2x=4xy$

$2,\left(x+y\right)^3-\left(x-y\right)^3-2y^3$

$=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3$

$=6x^2y$

$3,\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\\ =\left[\left(x+y\right)-\left(x-y\right)\right]^2\\ =\left(x+y-x+y\right)^2\\ =4y^2$

$4,\left(2x+3\right)^2-2\left(2x+3\right)\left(2x+5\right)+\left(2x+5\right)^2\\ =\left[\left(2x+3\right)-\left(2x+5\right)\right]^2\\ =\left(2x+3-2x-5\right)^2\\ =\left(-2\right)^2\\ =4$

$5,9^8.2^8-\left(18^4+1\right)\left(18^4-1\right)\\ =18^8-\left[\left(18^4\right)^2-1\right]\\ =18^8-18^8+1\\ =1$

Đúng(2)

NL

Nguyễn Lê Phước Thịnh

29 tháng 6 2023

1: =x^2+2xy+y^2-x^2+2xy-y^2=4xy

2: =x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3

=6x^2y

3: =(x+y-x+y)^2=(2y)^2=4y^2

4: =(2x+3-2x-5)^2=(-2)^2=4

5: =18^8-18^8+1=1

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

20 tháng 9 2023

Rút gọn các biểu thức đại số sau:

a) $6(y - x) - 2(x - y)$

b) $3{x^2} + x - 4x - 5{x^2}$

#Toán lớp 7

1

HQ

Hà Quang Minh

Giáo viên

20 tháng 9 2023

a) Cách 1:

$6(y - x) - 2(x - y)$

$ = 6y - 6x - 2x + 2y$

$ = 8y - 8x$

Cách 2:

$6(y - x) - 2(x - y)\\= 6(y-x)+2(y-x)\\=(6+2).(y-x)\\=8.(y-x)\\=8y-8x$

b) $3{x^2} + x - 4x - 5{x^2}$

$ = (3{x^2} - 5{x^2}) + (x - 4x)$

$ = - 2{x^2} - 3x$

Đúng(0)

T

Tears

22 tháng 6 2018 - olm

Rút gọn biểu thức

a) A= 39(x-y)^2-2(x+y)^2-(x-y)(x+y)

b) B= (x-1)^2-2(x-1)(x-3)+(x-3)^2

c) C= (2x+3)^2+(2x+3)(2x-6)+(x-3)^2

d) D= (x^2+x+1)(x^2-x+1)(x^4-x^2+1)(x^8-x^4+1)

#Toán lớp 8

0

UB

Ú Bé Heo (ARMY BLINK)

23 tháng 7 2021

Kết quả sau khi rút gọn biểu thức A = (x – y – 1)³ – (x – y + 1)³ + 6(x – y)² là: …

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

23 tháng 7 2021

Ta có: $A=\left(x-y-1\right)^3-\left(x-y+1\right)^3+6\left(x-y\right)^2$

$=\left(x-y-1-x+y-1\right)\left[\left(x-y-1\right)^2+\left(x-y-1\right)\left(x-y+1\right)+\left(x-y+1\right)^2\right]+6\left(x-y\right)^2$

$=-2\cdot\left[3\left(x-y\right)^2+1\right]+6\left(x-y\right)^2$

$=-6\left(x-y\right)^2+6\left(x-y\right)^2-2$

=-2

Đúng(1)

NL

Nguyễn Lê Thành Tín

23 tháng 10 2017 - olm

Rút gọn biểu thức

3(x-y)^2-2(x+y)^2-(x-y)(x+y)

#Toán lớp 8

0

TT

Tạ Thu Hương

24 tháng 7 2020

Rút gọn biểu thức :
( x/2-y^3)^3 - 6(y-x/2)^2 - 12(y-x/2) - 8 khi x = 4, y = 2

#Toán lớp 8

1

AH

Akai Haruma

Giáo viên

27 tháng 7 2020

Lời giải:

$x=4$ thì $\frac{x}{2}=2=y$

$\Rightarrow y-\frac{x}{2}=0$

Do đó:

$(\frac{x}{2}-y^3)^3-6(y-\frac{x}{2})^2-12(y-\frac{x}{2})-8$

$=(\frac{x}{2}-y^3)^3-8=(2-2^3)^3-8=-224$

Đúng(0)

HN

Hoàng Nguyên

17 tháng 12 2022 - olm

Bài 1.Cho biểu thức
A = ($\dfrac{2-x}{x+3}-\dfrac{3-x}{x+2}+\dfrac{2-x}{x^2+5x+6}$) : (1-$\dfrac{x}{x-1}$)
(a) Rút gọn A.
(b) Tìm x để A > 2.

Bài 2.Cho x+y=a,$x^2+y^2=b$.Tính $x^3+y^3$theo a và b

#Toán lớp 8

0

NH

Nguyên Hoàng

1 tháng 7 2021

rút gọn rồi tính giá trị biểu thức sau

a) (3x-2)²+2x(3x-2)x(3x+2)+(3x+2)²tại x =$\dfrac{-1}{3}$

^b)(x+y-7)²-2x(x+y-7)x(y-6)+(y+6) tại x=101

c) 4x² -20x+27 tại x = 52,5

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

1 tháng 7 2021

a) Ta có: $\left(3x-2\right)^2+2\left(3x-2\right)\left(3x+2\right)+\left(3x+2\right)^2$

$=\left(3x-2+3x+2\right)^2$

$=36x^2$(1)

Thay $x=-\dfrac{1}{3}$ vào biểu thức (1), ta được:

$36\cdot\left(-\dfrac{1}{3}\right)^2=36\cdot\dfrac{1}{9}=4$

b) Sửa đề: $\left(x+y-7\right)^2-2\cdot\left(x+y-7\right)\left(y-6\right)+\left(y-6\right)^2$

Ta có: $\left(x+y-7\right)^2-2\cdot\left(x+y-7\right)\left(y-6\right)+\left(y-6\right)^2$

$=\left(x+y-7-y+6\right)^2$

$=\left(x-1\right)^2=100^2=10000$

Đúng(2)

HP

Hương Phùng

12 tháng 7 2021

B4: Rút gọn biểu thức:

a, $\dfrac{x^2}{y^2}\div\sqrt{\dfrac{x^2}{y^4}}$ với x,y $\ne$ 0

b, $\sqrt{\dfrac{27(x-1)^2}{12}}+\dfrac{3}{2}-(x-2)\sqrt{\dfrac{50x^2}{8(x-2)^2}}$ với 1<x<2

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

12 tháng 7 2021

a) Ta có: $\dfrac{x^2}{y^2}:\sqrt{\dfrac{x^2}{y^4}}$

$=\dfrac{x^2}{y^2}:\dfrac{x}{y^2}$

=x

b) Ta có: $\sqrt{\dfrac{27\left(x-1\right)^2}{12}}+\dfrac{3}{2}-\left(x-2\right)\sqrt{\dfrac{50x^2}{8\left(x-2\right)^2}}$

$=\sqrt{\dfrac{9}{4}}\cdot\sqrt{\left(x-1\right)^2}+\dfrac{3}{2}-\left(x-2\right)\cdot\sqrt{\dfrac{25}{4}}\cdot\sqrt{\dfrac{x^2}{\left(x-2\right)^2}}$

$=\dfrac{3}{2}\cdot\left(x-1\right)+\dfrac{3}{2}-\left(x-2\right)\cdot\dfrac{5}{2}\cdot\dfrac{x}{2-x}$

$=\dfrac{3}{2}x-\dfrac{3}{2}+\dfrac{3}{2}-\dfrac{5}{2}\left(x-2\right)\cdot\dfrac{-x}{x-2}$

$=\dfrac{3}{2}x+\dfrac{5}{2}\cdot\left(x\right)$

=4x

Đúng(2)

HP

Hương Phùng

13 tháng 7 2021

em cảm ơn ạ