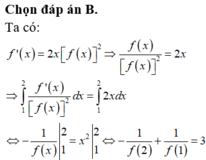cho hàm số y=f(x) thỏa mãn x(f).(x-2)=(x-4).f(x) với mọi giá trị của x. Hãy chứng minh rằng có ít nhất 2 giá trị của x để hàm số có giá trị =0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
Đoàn Đức Hà
Giáo viên
7 tháng 11 2021
\(\left(x+1\right)f\left(x+2\right)=\left(x-4\right)f\left(x-1\right)\)(1)
Thế \(x=4\)vào (1) ta được:
\(\left(4+1\right)f\left(4+2\right)=\left(4-4\right)f\left(4-1\right)\Leftrightarrow5f\left(6\right)=0\Leftrightarrow f\left(6\right)=0\)
Thế \(x=-1\)vào (1) ta được:
\(\left(-1+1\right)f\left(-1+2\right)=\left(-1-4\right)f\left(-1-1\right)\Leftrightarrow f\left(-2\right)=0\)
Vậy có ít nhất hai giá trị là \(x=6\)và \(x=-2\)để \(f\left(x\right)=0\).
CM
9 tháng 9 2018
Chọn A
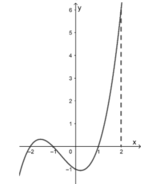
Từ đồ thị của hàm số y = f'(x) ta có bảng biến thiên của hàm số y = f(x) trên đoạn [-1;2] như sau
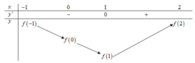
Nhận thấy
Để tìm 
ta so sánh f(-1) và f(2)
Theo giả thiết, 
Từ bảng biến thiên , ta có f(0) - f(1) > 0. Do đó f(2) - f(-1) > 0 
CM
28 tháng 7 2017
Chọn D
Ta có 3x.f(x) -
x
2
f
'
(
x
)
=
2
f
2
(
x
)
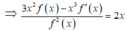
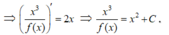
Thay x = 1 vào ta được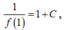 
vì f(1) =
1
3
nên suy ra C = 2
Nên 
Ta có: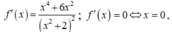 
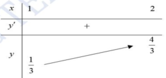
Khi đó, f(x) đồng biến trên [1;2]
Suy ra 
Suy ra 