√ − x 2 + 2 x − 1 xác định khi.... (giải thích rõ ràng giúp em vs ạ)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow\left\{{}\begin{matrix}a< 0\\\Delta\le0\end{matrix}\right.\)
Quy tắc: tam thức bậc 2 ko đổi dấu khi \(\Delta< 0\) (có dấu = hay ko phụ thuộc đề yêu cầu \(f\left(x\right)\) có dấu = hay ko)
Khi đã có \(\Delta< 0\) thì dấu \(f\left(x\right)\) chỉ còn phụ thuộc a. Nếu a dương thì \(f\left(x\right)\) dương trên R, nếu a âm thì \(f\left(x\right)\) âm trên R.

Ta có :\(\frac{x^7+x^6+x^5+x^4+x^3+x^2+1}{x^2-1}\)
\(=\frac{x^6\left(x+1\right)+x^4\left(x+1\right)+x^2\left(x+1\right)+\left(x+1\right)}{x^2-1}\)
\(=\frac{\left(x^6+x^4+x^2+1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(=\frac{\left(x^6+x^4+x^2+1\right)}{\left(x-1\right)}\)


\(B_2=\left\{x;x=2k,k\in N\right\}\)
\(B_4=\left\{x;x=4m,m\in N\right\}\)
Do \(4m=2.\left(2m\right)\Rightarrow B_4\subset B_2\)
\(\Rightarrow B_2\cap B_4=B_4\)

Bài `13`
\(a,\sqrt{27}+\sqrt{48}-\sqrt{108}-\sqrt{12}\\ =\sqrt{9\cdot3}+\sqrt{16\cdot3}-\sqrt{36\cdot3}-\sqrt{4\cdot3}\\ =3\sqrt{3}+4\sqrt{3}-6\sqrt{3}-2\sqrt{3}\\ =\left(3+4-6-2\right)\sqrt{3}\\ =-\sqrt{3}\\ b,\left(\sqrt{28}+\sqrt{12}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{84}\\ =\left(\sqrt{4\cdot7}+\sqrt{4\cdot3}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{4\cdot21}\\ =\left(2\sqrt{7}+2\sqrt{3}-\sqrt{7}\right)\cdot\sqrt{7}+2\sqrt{21}\\ =2\cdot7+2\sqrt{21}-7+2\sqrt{21}\\ =14+2\sqrt{21}-7+2\sqrt{21}\\ =7+4\sqrt{21}\)

Có: \(f\left(x\right)=2ax^2-4\left(bx-1\right)+5x+c-11\)
\(=2ax^2-4bx+4+5x+c-11\)
\(=2ax^2+\left(-4b+5\right)x+\left(c-11\right)\)
\(\Rightarrow f\left(x\right)=x^2-5x+6\Leftrightarrow\left\{{}\begin{matrix}2a=1\\-4b+5=-5\\c-11=6\end{matrix}\right.\) (theo đồng nhất hệ số)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=\dfrac{5}{2}\\c=17\end{matrix}\right.\)
 đây làm giúp em:>:> và giải thích rõ ràng giúp em ạ
đây làm giúp em:>:> và giải thích rõ ràng giúp em ạ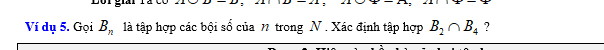

Khi \(x\in R\)
\(\sqrt{-x^2+2x-1}=\sqrt{-\left(x^2-2x+1\right)}=\sqrt{-\left(x-1\right)^2}\)
Do \(-\left(x-1\right)^2\le0\forall x\)
Nên căn thức chỉ xác định khi x=1