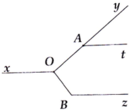
Cho hình vẽ bên, biết y A t ^ = 40°, x O y ^ = 140°, O B z ^ = 130° và OA ⊥ OB. Chứng minh At // Bz
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để chứng minh rằng AB//CD, ta cần sử dụng các thông tin đã cho về hình 4.16. Từ thông tin đã cho, ta biết rằng A = 130' và B = 140', và OA vuông góc với OB. Tuy nhiên, không có thông tin về các đỉnh khác của hình 4.16. Vì vậy, chúng ta không thể chứng minh rằng AB//CD chỉ dựa trên thông tin đã cho.

Ta có \(\left\{{}\begin{matrix}\widehat{O_1}+\widehat{O_2}=180^0\left(kề.bù\right)\\\widehat{O_3}+\widehat{O_4}=180^0\left(kề.bù\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\widehat{O_2}=180^0-140^0=40^0\\\widehat{O_4}=180^0-130^0=150^0\end{matrix}\right.\)
\(\widehat{AOB}=\widehat{O_2}+\widehat{O_4}=40^0+50^0=90^0\\ \Rightarrow OA\perp OB\)

Vì O A ⊥ O C nên A O C ^ = 90 ° . Trong góc AOC vẽ tia Ot sao cho O t / / A B .
Khi đó A ^ + A O t ^ = 180 ° (cặp góc trong cùng phía).
Suy ra A O t ^ = 180 ° − 130 ° = 50 ° .
Vì A O C ^ = 90 ° nên C O t ^ = 40 ° .
Ta có C ^ + C O t ^ = 140 ° + 40 ° = 180 ° .
Do đó CD // Ot (vì có cặp góc trong cùng phía bù nhau).
Suy ra AB // CD (vì cùng song song với Ot).

O A B C X Y Z
Xét 3 tứ giác OAXC ; OBYA ; OBZC có :
X + XAO + OCX + AOC = 3600 (Tứ giác OAXC)
Y + OAY + AOB + OBY = 3600 (Tứ giác OBYA)
Z + OCZ + COB + OBZ = 3600 (Tứ giác OBZC)
Dựa vào dữ kiện các góc bằng nhau , ta suy ra
Góc X = Góc Y = Góc Z
=> Tam giác XYZ đều
=> y O x ' ^ = y A t ^ (hai góc đồng vị bằng nhau)
=> Ox' // At (1).
Mặt khác: OA ⊥ OB => A O B ^ = 90 °
=> x ' O B ^ = y O B ^ − y O x ' ^ = 90 ° − 40 ° = 50 °
=> x ' O B ^ = O B z ^ = 50 ° + 130 ° = 180 °
(hai góc trong cùng phía bù nhau)
=>Ox' //Bz (2).
Từ (1) và (2), suy ra At //Bz